Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lực đóng vai trò là lực hướng tâm trong trường hợp trên là lực căng.
=> Vận tốc cực đại của vật để dây không bị đứt là:
\(\begin{array}{l}{T_{\max }} = {F_{ht\max }} = m.\frac{{v_{\max }^2}}{R}\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.R}}{m}} = \sqrt {\frac{{50.1,5}}{{0,5}}} \approx 12,23(m/s)\end{array}\)

Ta có lực căng dây đóng vai trò là lực hướng tâm
Do khối lượng và bán kính của vật chuyển động xung quanh bàn không đổi nên lực căng phụ thuộc vào tốc độ góc. Lực căng dây lớn nhất khi tốc độ góc lớn nhất
Ta có: m = 3 kg; R = 0,8 m; \({\omega _{\max }}\)= 1,6 vòng/s = 1,6.2π = 10 rad/s.
=> Lực căng dây lớn nhất là: \({T_{\max }} = {F_{ht\max }} = m.\omega _{\max }^2.R = {3.10^2}.0,8 = 240(N)\).

Chọn hệ quy chiếu như hình vẽ
Theo định luật II Newton ta có: \(\overrightarrow P + \overrightarrow T = \overrightarrow {{F_{ht}}} \) (1)
Từ hình vẽ ta có: R = l.sinα
Chiếu (1) lên trục Ox có:
\(\begin{array}{l}T.\sin \alpha = {F_{ht}}\\ \Leftrightarrow T.\sin \alpha = m.\frac{{{v^2}}}{R} \Leftrightarrow {v^2} = \frac{{T.\sin \alpha .R}}{m}\\ \Leftrightarrow {v^2} = \frac{{T.l.{{\sin }^2}\alpha }}{m} \Rightarrow {v_{\max }} \Leftrightarrow {T_{\max }},\sin \alpha = 1\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.l}}{m}} = \sqrt {\frac{{0,8.0,3}}{{0,2}}} \approx 1,1(m/s)\end{array}\)

Thay a=1,2m/s vào phương trình (b) ở câu trên, ta được: T 2 = 10.1 , 2 = 12 N
Nhận thấy: T 2 = T 1 = T = 12 N < T max = 15 N
=> Dây không bị đứt
Đáp án: C

Chọn D.
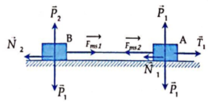
Áp dụng định luật II Niu-tơn cho hệ vật:
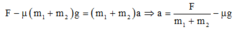
Áp dụng định luật II Niu-tơn cho vật B:
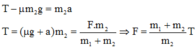
Do dây chỉ chịu được lực căng tối đa Tmax ⟹ T ≤ Tmax