Dựa vào phương trình chuyển động thẳng biến đổi đều, rút ra biểu thức (17.1).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Công thức chuyển động biến đổi đều: \(S=\dfrac{1}{2}at^2\) (1)
Công thức định luật II Niwton: \(F=ma\) (2)
Mà \(A=F\cdot S\) (3)
Thế (1), (2) vào (3) ta có
\(A=\dfrac{1}{2}\cdot m\cdot a^2\cdot t^2\) (4)
Mặt khác \(v=a\cdot t\)
\(\Rightarrow a^2\cdot t^2=v^2\) (5)
Thế (5) vào (4) \(A=\dfrac{1}{2}\cdot mv^2\)
VT
10 tháng 4 2019
* Phương trình chuyển động: x = x 0 + v 0 t + 1 2 a t 2 ,
Trong đó: x 0 và v 0 là tọa độ và vận tốc ban đầu, a là gia tốc.
Nếu x 0 = 0 thì phương trình có dạng đơn giản: x = v 0 t + 1 2 a t 2 .
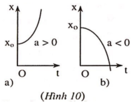
* Đồ thị của tọa độ theo thời gian trong chuyển động thẳng biến đổi đều:
Xét phương trình chuyển động có dạng: x = x 0 + 1 2 a t 2 .
Đường biểu diễn có phần lõm hướng lên trên nếu a > 0 , phần lõm hướng xuống dưới nếu a < 0 .(Hình 10a,b).
VT
29 tháng 11 2018
Chọn D.
Phương trình chuyển động thẳng biến đổi đều: x = x 0 + v 0 t + 1 2 a t 2
VT
10 tháng 7 2017
Chọn A.
Phương trình tổng quát của vận tốc trong chuyển động thẳng biến đổi đều v = v0 + at.
VT
28 tháng 7 2019
Chọn A.
Phương trình tổng quát của vận tốc trong chuyển động thẳng biến đổi đều v = v0 + at.
.
. Chuyển động nầy là chuyển động thẳng . 
HD: 
lấy giá trị dương , a lấy giá trị âm . B. 
đều lấy giá trị dương .
.
HD:
.
Thay 
B. 
C. 
D. 
Chuyển động của vật ném lên thẳng đứng cũng là CĐT BĐĐ 
.
Đối chiếu với : 
và 
B. 
D. 
và 
B. 
C. 
D. 
, thì
Biểu thức (17.1): \(A = F.s = \frac{1}{2}.m.{v^2}\)
Ban đầu vật đứng yên nên v0 = 0
Ta có:
\(F = m.a = m.\frac{{{v^2} - v_0^2}}{{2.s}} = \frac{{m.{v^2}}}{{2.s}}\)
=> \(A = F.s = \frac{{m.{v^2}}}{{2.s}}.s = \frac{1}{2}.m{v^2}\)