Cho a,b,c là số thực,a+b+c=3,d+e+f=3.ad+be+cf=3.Cmr a+b+c+d+e+f
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



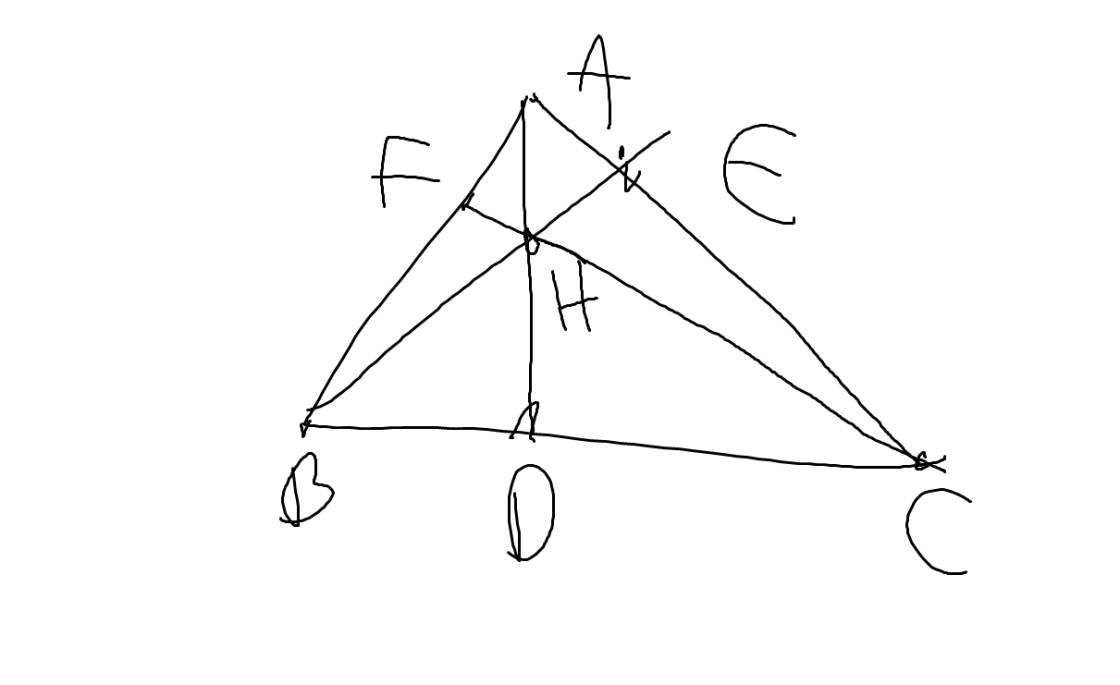
1: Xét tứ giác AFDC có
\(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
2: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
3:
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
4: Xét tứ giác HECD có
\(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
=>HECD là tứ giác nội tiếp

\(a,\left\{{}\begin{matrix}BF//GE\left(gt\right)\\FG//BE\left(gt\right)\end{matrix}\right.\Rightarrow BFGE\) là hbh \(\Rightarrow BF=GE\)
Mà \(BF=AF\left(F.là.trung.điểm.AB\right)\Rightarrow AF=GE\)
Mà \(AF//GE(BF//GE)\)
Do đó \(AFEG\) là hbh
\(b,\left\{{}\begin{matrix}BD=DC\\AE=EC\end{matrix}\right.\Rightarrow ED\) là đtb tg ABC \(\Rightarrow ED//AB\)
Mà \(EG//AB\left(gt\right)\)
Theo tiên đề Ơ-clít ta được EG trùng ED hay E,G,D thẳng hàng
\(c,\) ED là đtb tg ABC nên \(ED=\dfrac{1}{2}AB=AF=BF=GE\left(cm.trên\right)\)
Do đó E là trung điểm GD
Mà E là trung điểm AC nên ADCG là hbh
Do đó \(CG=AD\)

A B C D E F
Xét tam giác vuông ABC, theo hệ thức lượng: \(BD=\frac{c^2}{a}.\)
Xét tam giác vuông BDA, ta có: \(m=EB=\frac{BD^2}{BA}=\frac{c^3}{a^2}\)
Hoàn toàn tương tự: \(n=\frac{b^3}{a^2}\)
Vậy thì \(a.m.n=\frac{b^3.c^3}{a^3}\)
Lại có: \(bc=ah\Rightarrow\frac{bc}{a}=h\Rightarrow\frac{b^3c^3}{a^3}=h^3\Rightarrow a.m.n=h^3.\)