Cho tam giác ABC vuông tại A. Trên cạnh BC, lấy điểm K sao cho BK = BA. Gọi H là trung điểm AK. Trên tia đối của tia AB, lấy điểm D sao cho AD = KC. Chứng minh rằng:
a) Vẽ hình
b) Tam giác AHB bằng tam giác KHB
c) BK vuông góc với AK
c) AK // DC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔADM có
AB=AD
AM chung
BM=DM
Do đó: ΔABM=ΔADM

a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: Xét tứ giác ABMC có
H là trung điểm của AM
H là trung điểm của BC
Do đó: ABMC là hình bình hành
Suy ra: AB//MC
a: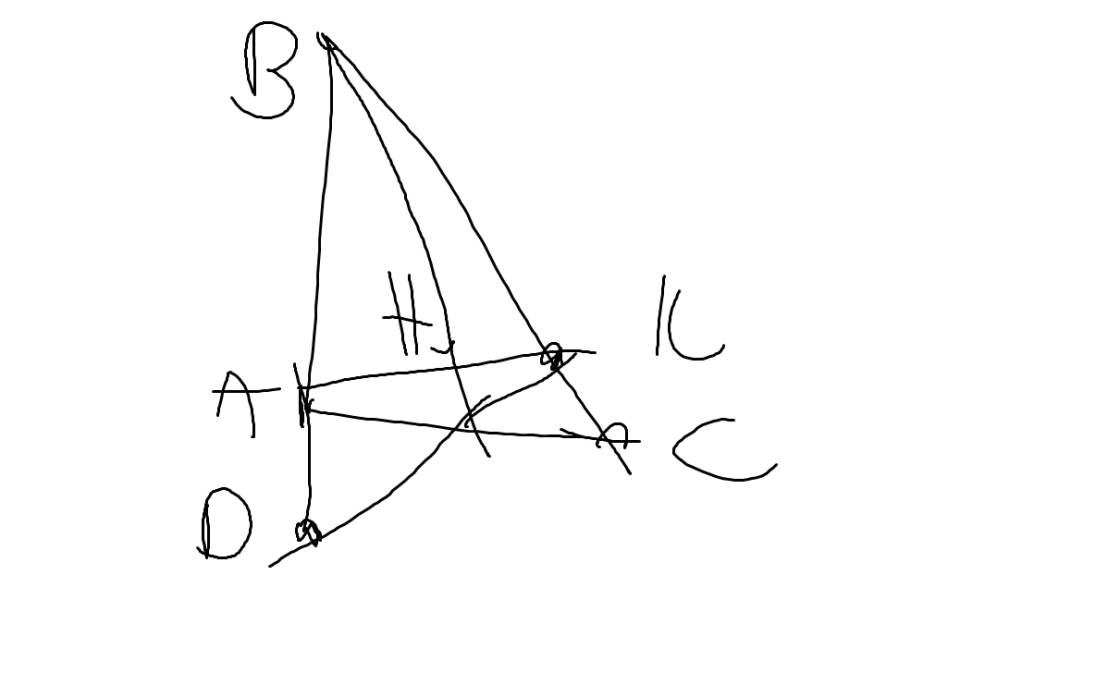
b: Xét ΔBAH và ΔBKH có
BA=BK
AH=KH
BH chung
Do đó: ΔBAH=ΔBKH
c: Sửa đề: Cm BH\(\perp\)AK
Ta có: ΔBAK cân tại B
mà BH là đường trung tuyến
nên BH là đường cao
=>BH\(\perp\)AK
d: Xét ΔBDC có \(\dfrac{BA}{AD}=\dfrac{BK}{KC}\)
nên AK//DC