GIúp mình bài hình này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ

\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

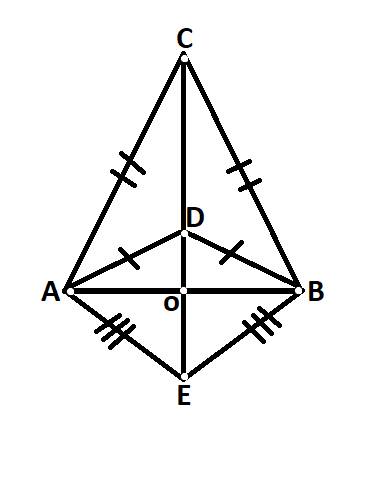
CA=CB
DA=DB
Do đó: CD là trung trực của BA(1)
EA=EB
=>E nằm trên trung trực của AB(2)
Từ (1), (2) suy ra C,D,E thẳng hàng

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi

Bài 6:
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Xét ΔADM và ΔAEM có
AD=AE
\(\widehat{DAM}=\widehat{EAM}\)
AM chung
Do đó: ΔADM=ΔAEM
Suy ra: \(\widehat{ADM}=\widehat{AEM}=90^0\)
hay ME⊥AC

a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)


 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn




a: ta có: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Ta có: OA//BD
BC\(\perp\)OA
Do đó: BD\(\perp\)BC
=>ΔBDC vuông tại B
Ta có: ΔBDC vuông tại B
=>ΔBDC nội tiếp đường tròn đường kính CD
mà ΔBDC nội tiếp (O)
nên CD là đường kính của (O)
c: Xét (O) có
ΔDEC nội tiếp
DC là đường kính
Do đó: ΔDEC vuông tại E
=>EC\(\perp\)ED tại E
=>CE\(\perp\)AD tại E
Xét ΔCDA vuông tại C có CE là đường cao
nên \(AE\cdot AD=AC^2\left(1\right)\)
Xét ΔCOA vuông tại C có CH là đường cao
nên \(AH\cdot AO=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{EAH}\) chung
Do đó: ΔAEH đồng dạng vớiΔAOD
=>\(\widehat{AEH}=\widehat{AOD}\)
mà \(\widehat{AEH}+\widehat{DEH}=180^0\)(hai góc kề bù)
nên \(\widehat{DEH}+\widehat{AOD}=180^0\)
=>\(\widehat{DEH}+\widehat{DOH}=180^0\)
=>DEHO là tứ giác nội tiếp
=>\(\widehat{ODH}=\widehat{OEH}\)