Cho tứ diện S.ABCD.Gọi M,N là hai điểm trên cạnh AB,BC sao cho MN không song song AC.Tìm giao tuyến của (SMN) và (SAC);(SAN) và (SCM)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: \(B\in SB\)
\(B\in\left(ABC\right)\)
Do đó: \(B=SB\cap\left(ABC\right)\)
b: Chọn mp(SAB) có chứa BH
\(SA\subset\left(SAB\right)\)
\(SA\subset\left(SAC\right)\)
Do đó: \(\left(SAB\right)\cap\left(SAC\right)=SA\)
Gọi E là giao của BH và SA
=>E là giao điểm cần tìm
c: Chọn mp(SBC) có chứa BK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SAC\right)\)
Do đó: \(\left(SBC\right)\cap\left(SAC\right)=SC\)
Gọi F là giao của BK với SC
=>F là giao điểm cần tìm
d: Trong mp(SAC), gọi O là giao của HK với AC
mà \(AC\subset\left(ABC\right)\)
nên \(O=HK\cap\left(ABC\right)\)

1:
a: \(S\in SA\)
\(S\in SB\subset\left(SBC\right)\)
Do đó: \(S=SA\cap\left(SBC\right)\)
b: Chọn mp(SAB) có chứa SM
\(AB\subset\left(ABC\right)\)
\(AB\subset\left(SAB\right)\)
Do đó: \(AB=\left(SAB\right)\cap\left(ABC\right)\)
\(M\in AB\)
=>SM giao AB=M
=>\(M=SM\cap\left(ABC\right)\)
c: Chọn mp(BAC) có chứa MN
\(BC\subset\left(BAC\right)\)
\(BC\subset\left(SBC\right)\)
Do đó: (BAC) giao (SBC)=BC
mà \(BC\cap MN=N\)
nên \(N=MN\cap\left(SBC\right)\)
d: Chọn mp(ABC) có chứa MN
\(AC\subset\left(SAC\right)\)
\(AC\subset\left(ABC\right)\)
Do đó: \(AC=\left(SAC\right)\cap\left(ABC\right)\)
Gọi giao của MN và AC là E
=>\(E=MN\cap\left(SAC\right)\)

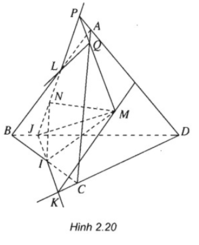
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
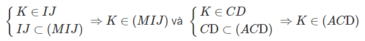
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
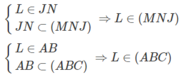
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
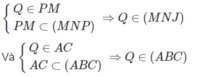
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).

a: Trong mp(ABC), gọi E là giao điểm của MN và BC
\(O\in\left(OMN\right);O\in\left(BCD\right)\)
=>\(O\in\left(OMN\right)\cap\left(BCD\right)\)
\(E\in MN\subset\left(OMN\right);E\in BC\subset\left(BCD\right)\)
=>\(E\in\left(OMN\right)\cap\left(BCD\right)\)
Do đó: \(\left(OMN\right)\cap\left(BCD\right)=OE\)
b: Chọn mp(BCD) có chứa DB
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi F là giao của OE với DB
=>F là giao của DB với mp(OMN)
Chọn mp(BCD) có chứa DC
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi K là giao của OE với DC
=>K là giao của DC với mp(OMN)
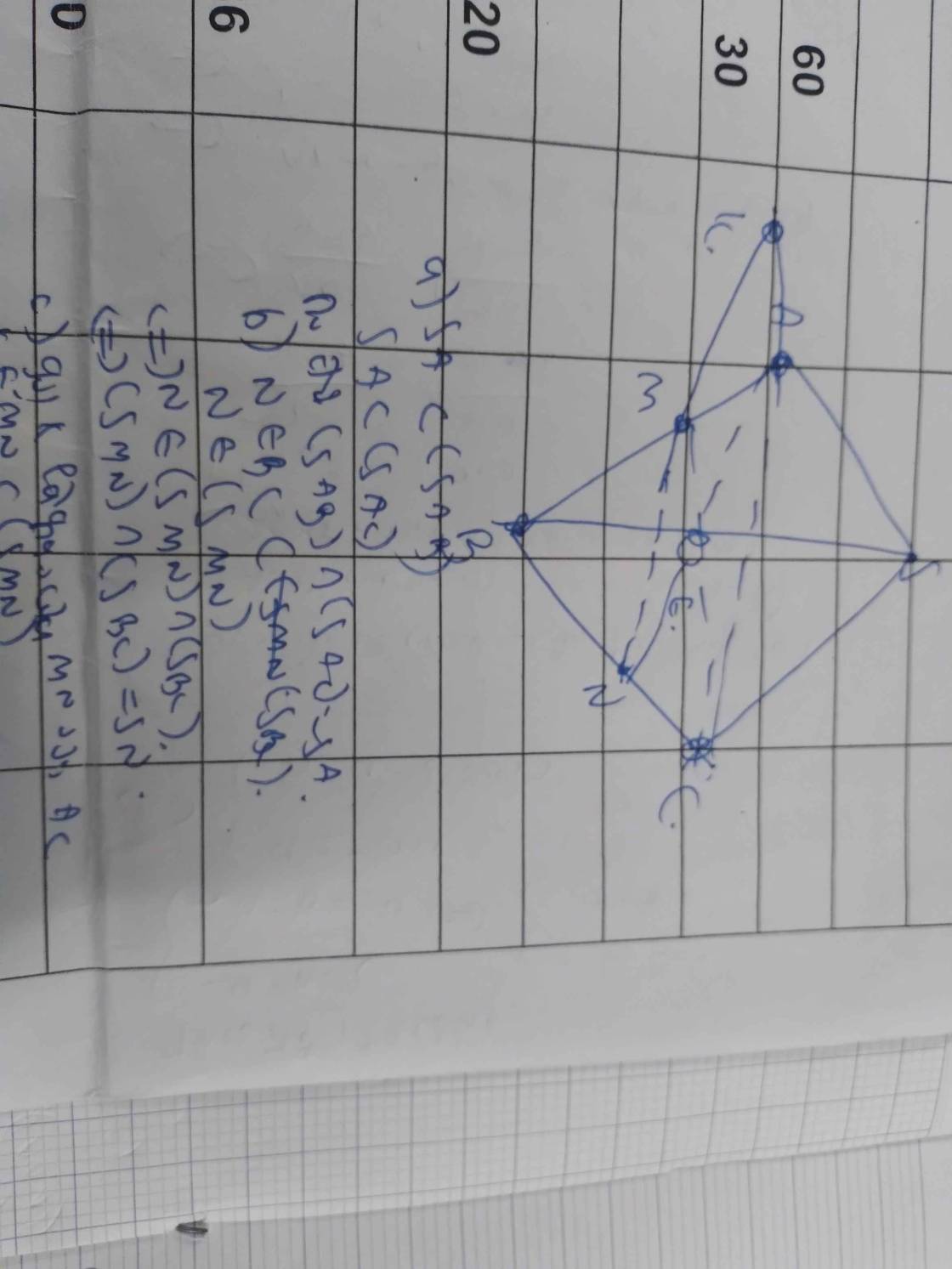
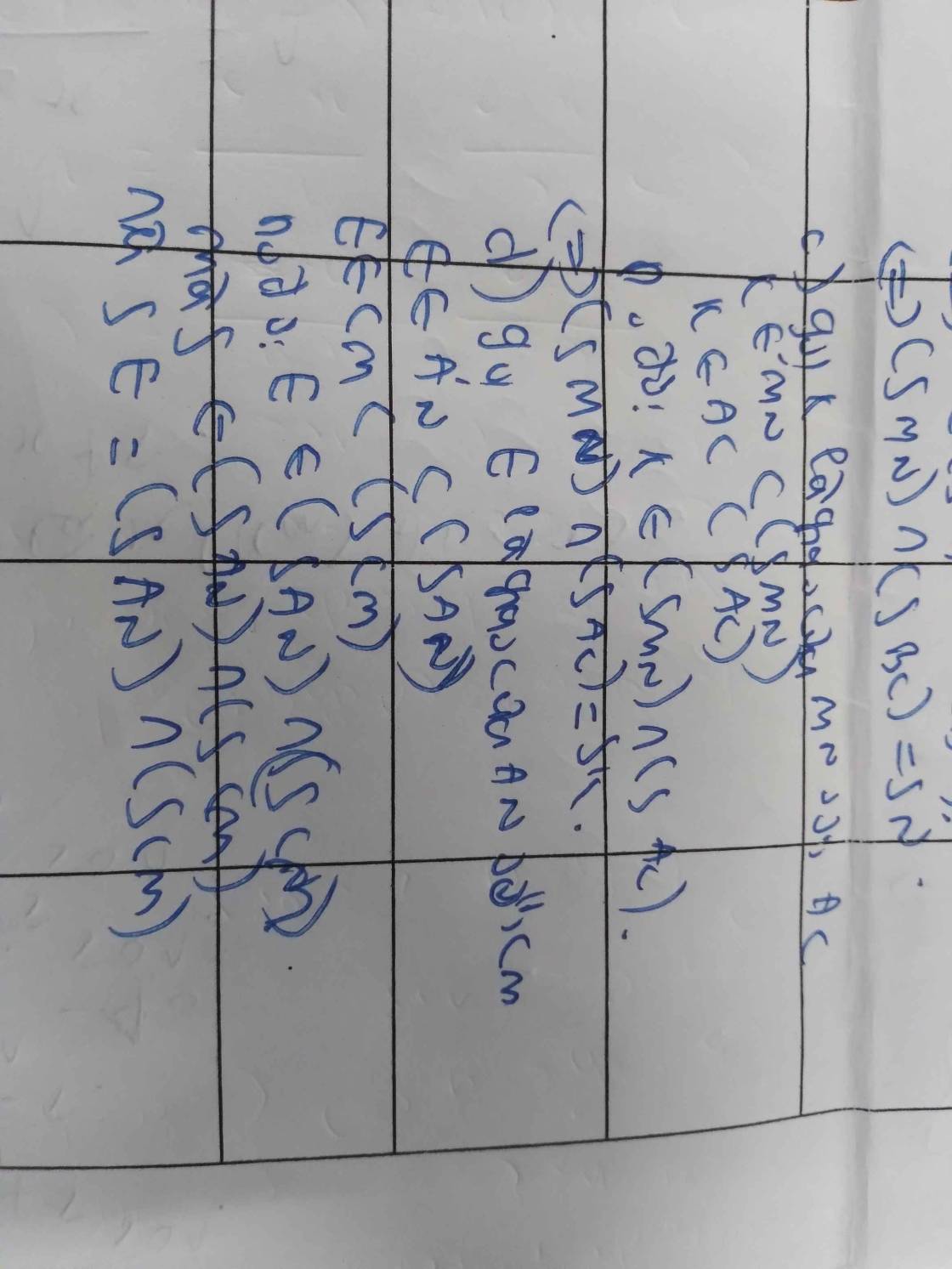

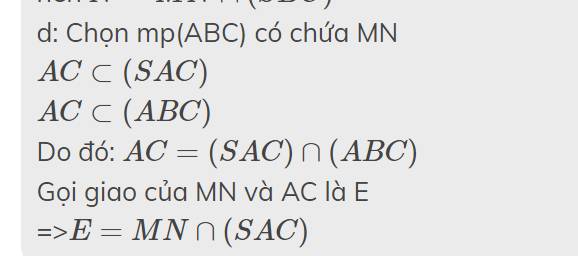


S \(\in\) (SMN) \(\cap\) (SAC) (1)
Trong mặt phẳng ABCD gọi L = AC \(\cap\) MN
Ta có: \(\left\{{}\begin{matrix}L\in MN,MN\subset\left(SMN\right)\\L\in AC,AC\subset\left(SAC\right)\end{matrix}\right.\) ⇒ L \(\in\) (SAC) \(\cap\) (SMN) (2)
Từ (1) và (2) ta có: (SAC) \(\cap\) (SMN) = SL
Ta có: S \(\in\) (SAN) \(\cap\) (SCM) (1)
Trong mặt phẳng ABCD gọi H = AN \(\cap\) CM
Vì: \(\left\{{}\begin{matrix}H\in AN,AN\subset\left(SAN\right)\\H\in CM,CM\subset\left(SCM\right)\end{matrix}\right.\) ⇒ H \(\in\) (SAN) \(\cap\) (SCM) (2)
Từ (1) và (2) ta có: (SAN) \(\cap\) (SCM) = SH