Cho tứ giác ABCD. Gọi M là điểm bất kì trên cạnh AB. Từ M vẽ các đường thẳng song song với AC và BD chúng cắt BC và AC lần lượt tại N và Q. Từ N vẽ đường thẳng song song với BD cắt AC tại P. Tứ giác MNPQ là hình gì ? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
20 tháng 10 2023
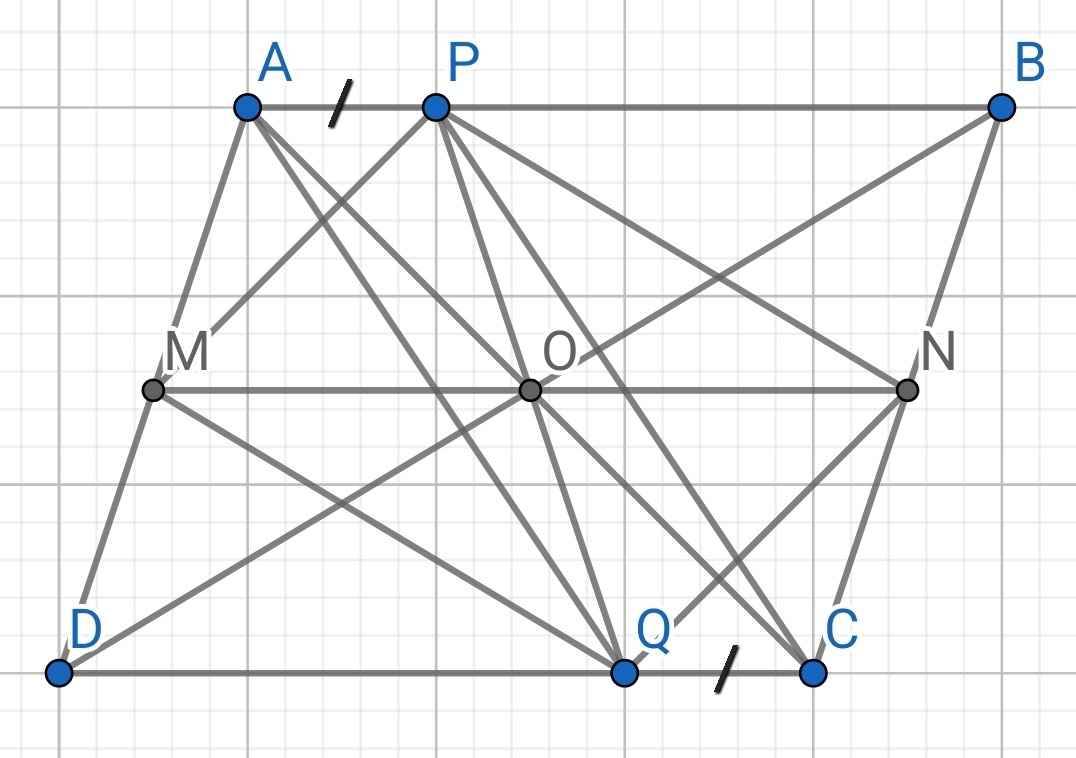a) *) Chứng minh AMNB là hình bình hành:
Do O là giao điểm của AC và BD
Mà ABCD là hình bình hành (gt)
⇒ O là trung điểm của AC và BD
Do MN // AB (gt)
⇒ OM // CD
∆ACD có
O là trung điểm AC
OM // CD
⇒ M là trung điểm AD
⇒ AM = AD : 2 (1)
Do MN // AB (gt)
⇒ ON // AB
∆ABC có:
O là trung điểm AC (cmt)
ON // AB (cmt)
⇒ N là trung điểm BC
⇒ BN = BC : 2 (2)
Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ AM // BN
Từ (1) và (2) ⇒ AM = BN
Tứ giác AMNB có:
AM // BN (cmt)
AM = BN (cmt)
⇒ AMNB là hình bình hành
*) Chứng minh APCQ là hình bình hành
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AP // CQ
Tứ giác APCQ có:
AP // CQ (cmt)
AP = CQ (gt)
⇒ APCQ là hình bình hành
c) Do O là trung điểm AC (cmt)
M là trung điểm AD (cmt)
⇒ OM là đường trung bình của ∆ACD
⇒ OM = CD : 2 (3)
Do O là trung điểm AC (cmt)
N là trung điểm BC (cmt)
⇒ ON là đường trung bình của ∆ABC
⇒ ON = AB : 2
Mà AB = CD (do ABCD là hình bình hành)
⇒ OM = ON
⇒ O là trung điểm MN
Do APCQ là hình bình hành (cmt)
O là trung điểm AC (cmt)
⇒ O là trung điểm PQ
Tứ giác MPNQ có:
O là trung điểm MN (cmt)
O là trung điểm PQ (cmt)
⇒ MPNQ là hình bình hành
⇒ MP // NQ và MQ = NP
Ta có: MQ//BD
NP//BD
Do đó: MQ//NP
Ta có: MN//AC
\(Q,P\in AC\)
Do đó: MN//PQ
Xét tứ giác MNPQ có
MQ//NP
MN//PQ
Do đó: MNPQ là hình bình hành