Giúp em bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)


Bài 4
Số giấy vụn khối 2 thu được là:
\(246-18=228\left(kg\right)\)
Số giấy vụn của khối 3 thu được là:
\(\dfrac{246+228}{2}=237\left(kg\right)\)
Trung bình mỗi khối thu được là:
\(\dfrac{246+228+237}{3}=237\left(kg\right)\)
Vậy.....
Bài 4 : Bài giải
Khối 2 thu được số kg giấy vụn là :
246 - 18 = 228 ( kg )
Khối 3 thu được số kg giấy vụn là :
( 246 + 228 ) : 2 = 237 ( kg )
Trung bình mỗi ngày thu được kg giấy vụn là :
( 246 + 228 + 237 ) : 3 = 237 ( kg )
Đáp số : 237 kg giấy vụn
Bài 5 Lười làm thông cảm :))

Tọa độ giao điểm A,B là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}x^2=2x+3\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)\left(x+1\right)=0\\y=2x+3\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(3;9\right);\left(-1;1\right)\right\}\)
vậy: A(3;9); B(-1;1)

a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)

\(\dfrac{2A}{2A+16.5}=\dfrac{43,66}{100}\)
=> \(200A=43,66.\left(2A+16.5\right)\)
=> \(200A-87,32A=3492,8\)
=> \(112,68A=3492,8\)
=> A= 31


\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)

a) \(A=x^4+4x+7=\left(x^2+4x+4\right)+3=\left(x+2\right)^2+3\ge3\)
\(minA=3\Leftrightarrow x=-2\)
b) \(B=x^2-x+1=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(minB=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
c) \(C=4x-x^2+3=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
\(maxC=7\Leftrightarrow x=2\)
d) \(D=2x-2x^2-5=-2\left(x^2-x+\dfrac{1}{4}\right)-\dfrac{9}{2}=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}\le-\dfrac{9}{2}\)
\(maxD=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{1}{2}\)

 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
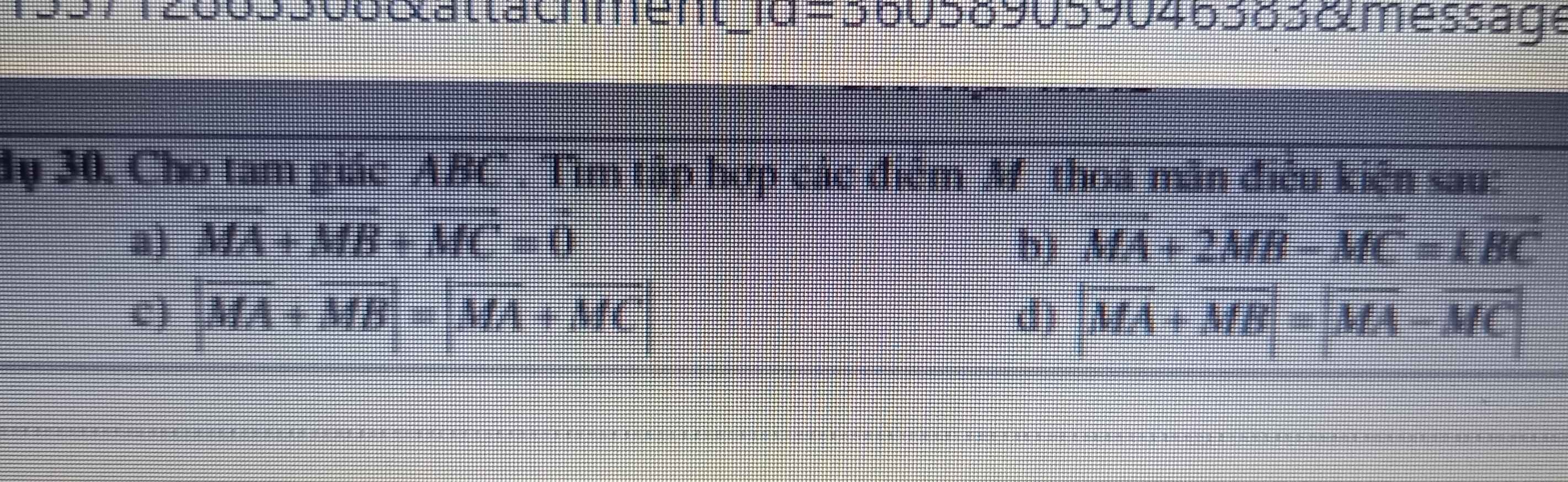


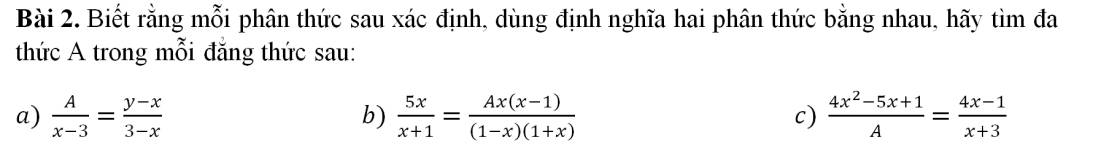 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 


 ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ giúp em bài này vs ạ em cảm ơn trc ạ
giúp em bài này vs ạ em cảm ơn trc ạ
a: \(G\in\left(SAD\right)\)
\(G\in GB\subset\left(GBC\right)\)
Do đó: \(G\in\left(SAD\right)\cap\left(GBC\right)\)
Xét (SAD) và (GBC) có
\(G\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó:(SAD) giao (SBC)=xy,xy đi qua G và xy//AD//BC
b: ABCD là hình bình hành tâm O
nên O là trung điểm chung của AC và BD
Xét ΔACB có
I,O lần lượt là trung điểm của CB,CA
=>IO là đường trung bình của ΔCAB
=>IO//AB
IO//AB
AB\(\subset\)(SAB)
IO không thuộc mp(SAB)
Do đó: IO//(SAB)
c: Xét ΔSAC có
H,O lần lượt là trung điểm của CS,CA
=>HO là đường trung bình của ΔSAC
=>HO//SA
HO//SA
SA\(\subset\)(SAB)
HO không nằm trong mp(SAB)
Do đó: HO//(SAB)
Ta có: IO//(SAB)
HO//(SAB)
IO,HO\(\subset\)(OHI)
Do đó: (OHI)//(SAB)