Cho đường tròn tâm (O) đường kính AB và một điểm C nằm trên đường tròn(C khác A và B).Gọi D là trung điểm AC
a,tính số đo OAD và chứng tỏ rằng OD//BC
b,Tiếp tuyến tại A của (O) cắt tia OD tại E.C/m EC là tiếp tuyến của (O)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

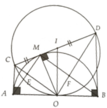
a, Dễ thấy A M B ^ = 90 0 hay E M F ^ = 90 0 tiếp tuyến CM,CA
=> OC ⊥ AM => O E M ^ = 90 0 Tương tự => O F M ^ = 90 0
Chứng minh được ∆CAO = ∆CMO => A O C ^ = M O C ^
=> OC là tia phân giác của A M O ^
Tương tự OD là tia phân giác của B O M ^ suy ra OC ⊥ OD <=> C O D ^
b, Do ∆AOM cân tại O nên OE là đường phân giác đồng thời là đường cao
=> O E M ^ = 90 0 chứng minh tương tự O F M ^ = 90 0
Vậy MEOF là hình chữ nhật
c, Gọi I là trung điểm CD thì I là tâm đường tròn đường kính CD và IO=IC=ID. Có ABDC là hình thang vuông tại A và B nên IO//AC//BD và IO vuông góc với AB. Do đó AB là tiếp tuyến của đường tròn đường kính CD.

a: Xét (O) có
DA là tiếp tuyến
DB là tiếp tuyến
Do đó: OD là tia phân giác của góc AOB(1)
Xét (O) có
EA là tiếp tuyến
EC là tiếp tuyến
Do đó: OE là tia phân giác của góc AOC(2)
Từ (1) và (2) suy ra OD⊥OE

(Quá lực!!!)
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)
a: Đề bài này chưa đủ dữ kiện để tính góc OAC nha bạn
ΔOAC cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)AC và OD là phân giác của góc AOC
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB
mà OD\(\perp\)AC
nên OD//CB
b: Xét ΔOAE và ΔOCE có
OA=OC
\(\widehat{AOE}=\widehat{COE}\)
OE chung
Do đó: ΔOAE=ΔOCE
=>\(\widehat{OAE}=\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)
mik nhầm bạn ơi
ở câu b là tính số đo góc ODA....