Cho tam giác ABC. Xác định vị trí điểm M,N,P,Q thỏa mãn. giúp mình với ạ, đặc biệt là câu d ạ. 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

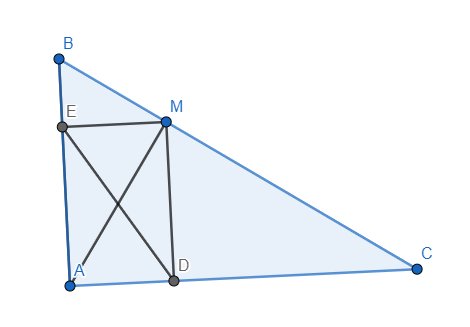
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC.

Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P

Vẽ MH ^ BC, BK ^ AC.
SAMNB = 3SMNC
Þ SABC = 4SMNC
Ta có: S A B C S B M C = A C M C = 3 2
S B M C S M N C = B C N C = 6 N C ⇒ S A B C S M N C = 9 N C
Mà SABC = 4SCMN Þ NC = 2,25
a: \(\overrightarrow{MA}=-3\cdot\overrightarrow{MB}\)
\(\overrightarrow{MA}+\overrightarrow{BM}=\overrightarrow{BA}\)
=>\(-3\cdot\overrightarrow{MB}-\overrightarrow{MB}=\overrightarrow{BA}\)
=>\(\overrightarrow{BA}=-4\overrightarrow{MB}=4\overrightarrow{BM}\)
=>M nằm giữa A và B sao cho BA=4BM
b:
Gọi E là trung điểm của AB
Vì E là trung điểm của AB nên \(\overrightarrow{NA}+\overrightarrow{NB}=2\cdot\overrightarrow{NE}\)
\(\overrightarrow{NA}+\overrightarrow{NB}+2\cdot\overrightarrow{NC}=\overrightarrow{0}\)
=>\(2\cdot\overrightarrow{NE}+2\cdot\overrightarrow{NC}=\overrightarrow{0}\)
=>\(\overrightarrow{NE}+\overrightarrow{NC}=\overrightarrow{0}\)
=>N là trung điểm của CE
c: \(\left|\overrightarrow{PA}\right|=\left|\overrightarrow{PB}\right|\)
=>\(\left[{}\begin{matrix}\overrightarrow{PA}=-\overrightarrow{PB}\\\overrightarrow{PA}=\overrightarrow{PB}\left(loại\right)\end{matrix}\right.\)
=>\(\overrightarrow{PA}=-\overrightarrow{PB}\)
=>P là trung điểm của AB