Hình vuông ABCD có cạnh bằng a.Gọi E là trung điểm cạnh BC, F là trung điểm AE.Tìm độ dài đoạn thẳng DF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


E là trung điểmcủa BC
=>EB=EC=a/2
\(AE=\sqrt{AB^2+BE^2}=\dfrac{a\sqrt{5}}{2}\)
Xét ΔABE vuông tại B có \(\left\{{}\begin{matrix}cosBAE=\dfrac{AB}{AE}=\dfrac{a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{2}{\sqrt{5}}\\sinBAE=\dfrac{BE}{AE}=\dfrac{0.5a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
=>\(cosDAF=cosBEA=sinBAE=\dfrac{1}{\sqrt{5}}\)
\(AF=\dfrac{AE}{2}=\dfrac{a\sqrt{5}}{4}\)
Xét ΔADF có \(cosDAF=\dfrac{AD^2+AF^2-DF^2}{2\cdot AD\cdot AF}\)
=>\(\dfrac{a^2+a^2\cdot\dfrac{5}{16}-DF^2}{2\cdot\dfrac{a\sqrt{5}}{4}\cdot a}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{\dfrac{21}{16}a^2-DF^2}{\dfrac{a^2\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{21}{16}a^2-DF^2=\dfrac{a^2}{2}\)
=>\(DF^2=\dfrac{13}{16}a^2\)
=>\(DF=\dfrac{a\sqrt{13}}{4}\)

Trong mp(BCD) gọi \(I=FG\cap BD\)
Trong mp (ADB) gọi \(H=IE\cap AD\)
Khi đó HG = \(\left(EFG\right)\cap\left(ACD\right)\)
Áp dụng định lí menelaus cho tam giác BCD với 3 giao điểm I,G,F thẳng hàng ta có:
\(\dfrac{ID}{IB}.\dfrac{FB}{FC}.\dfrac{GC}{GD}=1=>\dfrac{ID}{IB}=\dfrac{1}{4}\)
Xét tam giác ABD với 3 điểm thẳng hàng I,H,E thẳng hàng ta có:
\(\dfrac{HD}{HA}.\dfrac{EA}{EB}.\dfrac{IB}{ID}=1\) => \(\dfrac{HD}{HA}=\dfrac{1}{4}=>HD=\dfrac{a}{5}\)
Xét tam giác HDG:
\(HG^2=HD^2+DG^2-2DH.DG.cos60^o=\dfrac{a^2}{25}+\dfrac{a^2}{9}-\dfrac{a^2}{15}=\dfrac{19a^2}{225}\)
=> HG \(=\dfrac{\sqrt{19}}{15}a\)

\(\overrightarrow{AM}\cdot\overrightarrow{BC}=\overrightarrow{BC}\left(\overrightarrow{BM}-\overrightarrow{BA}\right)=\overrightarrow{BM}\cdot\overrightarrow{BC}-\overrightarrow{BC}\cdot\overrightarrow{BA}\)
\(=BM\cdot BC\cdot cos0^0=\dfrac{1}{2}\cdot a^2\cdot1=\dfrac{1}{2}a^2\)
\(\left|\overrightarrow{AM}+\overrightarrow{BC}\right|=\sqrt{AM^2+BC^2+2\cdot\dfrac{1}{2}a^2}\)
\(=\sqrt{\dfrac{1}{4}a^2+a^2+a^2+a^2}=\dfrac{\sqrt{13}}{2}\cdot a\)

a. Chứng minh tam giác BCE = tam giác CDF (cgc): BE = CF=1/2 a ; góc B = góc C = 90 độ ; BC = CD= a
=> góc ECB = góc FDC => tam giác FCM đồng dạng với tam giác FDC (gg)
=> góc DCF = góc CMF =90 độ
=> đpcm
b.tam giác FCM đồng dạng với tam giác FDC => CM/CD=CF/DF
=> CD=CM.DF/CF hay a=CM.CE/CF ( vì DF =CE bởi tam giác BCE = tam giác CDF)
c.Chứng minh tam giác BCE = tam giác AKE (gcg):góc CEB = góc KEA ; BE = AE=1/2 a ; góc B = góc A = 90 độ
=> BC = AK = a => AD = AK => A là trung điểm của tam giác MKD
=> DA = AM => tam giác MAD cân tại A
d.CM/CD=CF/DF => CM = CF.CD/DF hay (1/4.a^2)/DF
tam giác DMC đồng dạng với tam giác DCF (gg)=>DM/DC=DC/DF =>DM=DC.DC/DF hay DM=a^2/DF
=>CM.DM=(1/4 . a^4)/DF^2
tính được DF^2=5/4a^2
=> CM.DM=(1/4 . a^4)/(5/4a^2)=1/5.a^2
=>SDMC= 1/2.CM.DM=1/10.a^2

Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)

Đáp án C.
Hướng dẫn giải:
Ta có
![]()
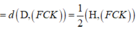
Kẻ H I ⊥ C K , H J ⊥ F I
![]()
Ta có H I = 2 a 5 5
![]()
⇒ S B = a 3
![]()
⇒ H F = a 2 2
Ta có 1 H J 2 = 1 H I 2 + 1 H F 2 = 13 4 a 2
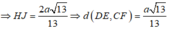
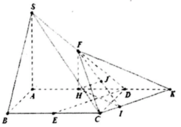
Có :
\(\text{AE = DE = }\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
Dùng công thức độ dài trung tuyến:
\(DF^2=\dfrac{DA^2+DE^2}{2}-\dfrac{AE^2}{4}=\dfrac{a^2+\dfrac{5a^2}{4}}{2}-\dfrac{5a^2}{16}=\dfrac{13a^2}{16}\) \(\Rightarrow\) \(DF=\dfrac{a\sqrt{13}}{4}\)