Rút gọn biểu thức
\(A=\dfrac{x^2}{5x+25}+\dfrac{2\left(x-5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: \(=2x^4-x^3-10x^2-2x^3+x^2+10x=2x^3-3x^3-9x^2+10x\)
b: \(=\left(x^2-15x\right)\left(x^2-7x+3\right)\)
\(=x^4-7x^3+3x^2-15x^3+105x^2-45x\)
\(=x^4-22x^3+108x^2-45x\)
c: \(=12x^5-18x^4+30x^3-24x^2\)
d: \(=-3x^6+2.4x^5-1.2x^4+1.8x^2\)

1) \(\dfrac{15-5x}{5x^2-15x}=\dfrac{5\left(3-x\right)}{5x\left(x-3\right)}=-\dfrac{5\left(x-3\right)}{5x\left(x-3\right)}=-\dfrac{1}{x}\)
Chọn A
2) \(\dfrac{x\left(x-5\right)}{x^2+25}=\dfrac{x\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{x}{x+5}\)
\(A=0\Leftrightarrow\dfrac{x}{x+5}=0\Leftrightarrow x=0\)
Chọn B
3) \(\dfrac{2x-5}{5-2x}=-\dfrac{5-2x}{5-2x}=-1\)
Chọn D

a: \(P=\dfrac{x\left(x+2\right)}{2\left(x+5\right)}+\dfrac{x-5}{x}-\dfrac{5x-50}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+2x^2+2x^2-50-5x+50}{2x\left(x+5\right)}\)
\(=\dfrac{x^3+4x^2-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)

\(B=\left(\dfrac{x}{x^2-25}-\dfrac{x-5}{x^2+5x}\right):\dfrac{2x-5}{x^2+5x}+\dfrac{x}{5-x}\) (1).
Đkxđ: \(x\ne\pm5;\)
(1) \(=\left(\dfrac{x}{\left(x+5\right)\left(x-5\right)}-\dfrac{x-5}{x\left(x+5\right)}\right):\dfrac{2x-5}{x\left(x+5\right)}+\dfrac{x}{5-x}\)
\(=\left(\dfrac{x^2-\left(x-5\right)\left(x-5\right)}{x\left(x+5\right)\left(x-5\right)}\right):\dfrac{2x-5}{x\left(x+5\right)}+\dfrac{x}{5-x}\)
\(=\dfrac{25}{x\left(x+5\right)\left(x-5\right)}.\dfrac{x\left(x+5\right)}{2x-5}-\dfrac{x}{x-5}\)
\(=\dfrac{25}{\left(x-5\right)\left(2x-5\right)}-\dfrac{x}{x-5}\)
\(=\dfrac{25-x\left(2x-5\right)}{\left(x-5\right)\left(2x-5\right)}\)
\(=\dfrac{25-2x^2+5x}{\left(x-5\right)\left(2x-5\right)}\)

a) ĐKXĐ: \(x\ne-10;x\ne0;x\ne-5\)
b) \(P=\dfrac{x^2+2x}{2x+20}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x^2+2x}{2\left(x+10\right)}+\dfrac{x-5}{x}+\dfrac{50-5x}{2x\left(x+5\right)}\)
\(=\dfrac{x\left(x^2+2x\right)\left(x+5\right)}{2x\left(x+10\right)\left(x+5\right)}+\dfrac{2\left(x-5\right)\left(x+10\right)}{2x\left(x+10\right)\left(x+5\right)}+\dfrac{\left(50-5x\right)\left(x+10\right)}{2x\left(x+5\right)\left(x+10\right)}\)
\(=\dfrac{x^4+7x^3+10x^2+2x^2+10x-100+500-5x^2}{2x\left(x+10\right)\left(x+5\right)}\)
\(=\dfrac{x^4+7x^3+7x^2+10x+400}{2x\left(x+10\right)\left(x+5\right)}\)
c) \(P=0\Rightarrow x^4+7x^3+7x^2+10x+400=0\Leftrightarrow...\)
Số xấu thì câu c, d làm cũng như không. Bạn xem lại đề.

a: ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
\(C=\dfrac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}=\dfrac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\dfrac{x-1}{2}\)

a: ĐKXĐ: x<>1; x<>2; x<>3
\(K=\left(\dfrac{x^2}{\left(x-2\right)\left(x-3\right)}+\dfrac{x^2}{\left(x-1\right)\left(x-2\right)}\right)\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{x^4+2x^2+1-x^2}\)
\(=\dfrac{x^3-x^2+x^3-3x^2}{\left(x-2\right)\left(x-3\right)\left(x-1\right)}\cdot\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x^2+1+x\right)\left(x^2+1-x\right)}\)
\(=\dfrac{2x^3-4x^2}{\left(x-2\right)}\cdot\dfrac{1}{\left(x^2+x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{2x^2\left(x-2\right)}{\left(x-2\right)\left(x^4+x^2+1\right)}=\dfrac{2x^2}{x^4+x^2+1}\)
b:
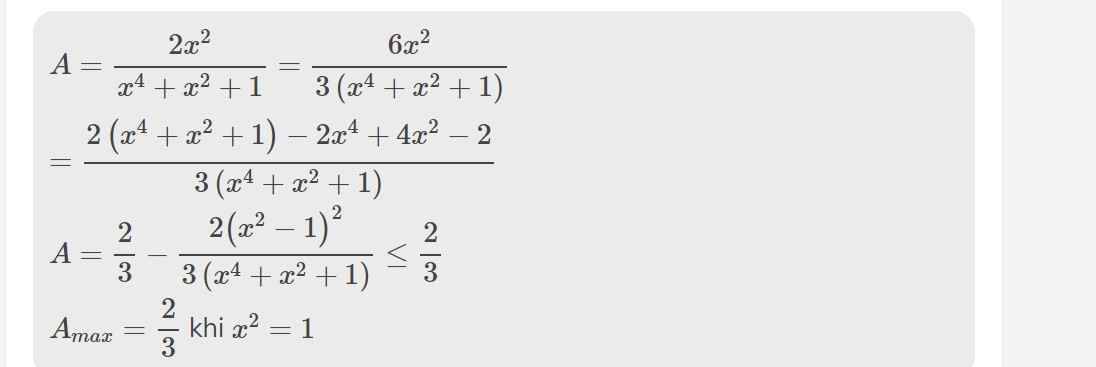

\(E=\dfrac{\left|x-3\right|}{\left(x-3\right)\left(x+3\right)}\left(x+3\right)^2=\dfrac{\left|x-3\right|\left(x+3\right)}{x-3}\left(x\ne\pm3\right)\)
Với \(x>3\Leftrightarrow E=x+3\)
Với \(x< 3\Leftrightarrow E=-x-3\)
\(F=\dfrac{x+5\sqrt{x}-10\sqrt{x}-5\sqrt{x}+25}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\left(x\ge0;x\ne25\right)\\ F=\dfrac{\left(\sqrt{x}-5\right)^2}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
ĐKXĐ: \(x\notin\left\{0;-5\right\}\)
\(A=\dfrac{x^2}{5x+25}+\dfrac{2\left(x-5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\)
\(=\dfrac{x^2}{5\left(x+5\right)}+\dfrac{2\left(x-5\right)}{x}+\dfrac{5x+50}{x\left(x+5\right)}\)
\(=\dfrac{x^3+2\cdot5\left(x-5\right)\left(x+5\right)+5\left(5x+50\right)}{5x\left(x+5\right)}\)
\(=\dfrac{x^3+10x^2-250+25x+250}{5x\left(x+5\right)}\)
\(=\dfrac{x^3+10x^2+25x}{5x\left(x+5\right)}=\dfrac{x\left(x^2+10x+25\right)}{5x\left(x+5\right)}\)
\(=\dfrac{\left(x+5\right)^2}{5\left(x+5\right)}=\dfrac{x+5}{5}\)
\(A=\dfrac{x^2}{5x+25}+\dfrac{2\left(x-5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\left(ĐKXĐ:x\ne0;x\ne-5\right)\)
\(A=\dfrac{x^2}{5\left(x+5\right)}+\dfrac{2\left(x-5\right)}{x}+\dfrac{50+5x}{x\left(x+5\right)}\)
\(A=\dfrac{x^2.x}{5x\left(x+5\right)}+\dfrac{2.5\left(x+5\right)\left(x-5\right)}{5x\left(x+5\right)}+\dfrac{5\left(50+5x\right)}{5x\left(x+5\right)}\)
\(A=\dfrac{x^3}{5x\left(x+5\right)}+\dfrac{10.\left(x^2-25\right)}{5x\left(x+5\right)}+\dfrac{250+25x}{5x\left(x+5\right)}\)
\(A=\dfrac{x^3}{5x\left(x+5\right)}+\dfrac{10x^2-250}{5x\left(x+5\right)}+\dfrac{250+25x}{5x\left(x+5\right)}\)
\(A=\dfrac{x^3+10x^2-250+250+25x}{5x\left(x+5\right)}\)
\(A=\dfrac{x^3+10x^2+25x}{5x\left(x+5\right)}\)
\(A=\dfrac{x\left(x^2+10x+25\right)}{5x\left(x+5\right)}\)
\(A=\dfrac{\left(x+5\right)^2}{5\left(x+5\right)}\)
\(A=\dfrac{x+5}{5}\)