Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.

Cách 2:
Gọi x là số dãy ghế lúc đầu (Đk:x và x là ước của 250, dãy)
Số chỗ ngồi ở mỗi dãy lúc đầu: 250/x (chỗ)
Số dãy ghế lúc sau là x + 3 (dãy). Số chỗ ngồi lúc sau: 308/(x+3) (chỗ).
Vì mỗi dãy ghế phải kê thêm 1 chỗ ngồi nữa thì vừa đủ ta có PT:
308/(x+3)-250/x=1↔x^2-55x+750=0↔[█(x_1=30 (loại) vì 250 không chia hết cho 30@x_2=25 (nhận))┤
Vậy lúc đầu có 25 dãy ghế. Mỗi dãy ghế có 10 chỗ ngồi.
Cách 1:
Gọi x là số dãy ghế lúc đầu; y là số người trên mỗi dãy ghế lúc đầu (x,y>0)
Ta có tổng cộng 250 người nên x.y =250 (1)
Nếu thêm 3 dãy ghế tức x + 3 thì mỗi dãy còn lại phải xếp thêm 1 người tức y + 1
Ta có: (x+3).(y+1) = 250 (2)
Từ (1) và (2) ta có hệ:
Vậy lúc đầu có 25 dãy ghế. Mỗi dãy ghế có 10 chỗ ngồi.

Gọi số ghế ở mỗi hàng ban đầu là x (ghế, x > 0)
Gọi số hàng ghế trong phòng ban đầu là y (hàng, y < 50)
Ta có x nhân y = 240
Khi tăng số ghế và số hàng ta có (x + 1)(y + 3)= 315
Ta có hệ phương trình {x nhân y= 240
{y + 3x = 72
Giải hệ phương trình ta có y= 12; x= 20
Vậy số dãy ghế có trong phòng lúc đầu là 12 hàng.

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có \(\frac{240}{x}\)ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=> \(\left(\frac{240}{x}+1\right)\left(x+3\right)=315\Leftrightarrow240+\frac{720}{x}+x+3=315\)
\(\Leftrightarrow x-72+\frac{720}{x}=0\Leftrightarrow\frac{x^2-72x+720}{x}=0\Leftrightarrow x^2-72x+720=0\)
\(\Delta'=\left(-36\right)^2-720=576\)
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.

Gọi số dãy ghế có trong phòng họp lúc đầu là x (x<50)
Lúc đầu mỗi dãy có ghế
Vì lúc sau có 315 người tham dự nên phải kê thêm 3 dãy, mỗi dãy thêm 1 ghế
=>
=> x1= 60 (Loại), x2=12 (thỏa mãn)
Vậy trong phòng họp lúc đầu có 12 dãy ghế.

Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]
=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)
Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2
Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)
Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)
=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a
=> 35a-70+2a\(^2\)-4a=35a
=> 2a\(^2\)-4a-70=0
=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp
Trường hợp 1 : a-1 = -6 => a = - 5 [loại]
Trường hợp 2 : a - 1 = 6 => a = 7
Còn đây bạn làm nốt tiếp
Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người

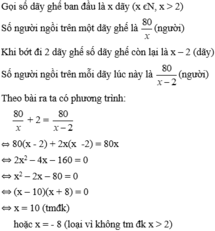
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.
Giải:
Phòng họp đó có số ghế là:
10 nhân 5 = 50 (cái ghế)
Vậy phòng họp đó đủ chỗ cho 50 người ngồi hợp (mỗi người 1 cái ghế)
k cho mik nha
10x5=50(ghế)
Vậy phòng họp đó đủ để chứa 50 người