Cho tam giác ABC, M là một điểm thuộc BC. Chứng minh 2AH2=MB2+MC2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 6 2017
a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
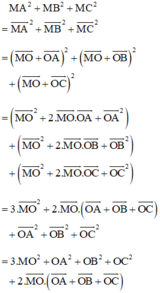
Lại có:
+ O là trọng tâm tam giác nên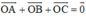 
+ Bán kính đường tròn ngoại tiếp tam giác:
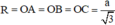
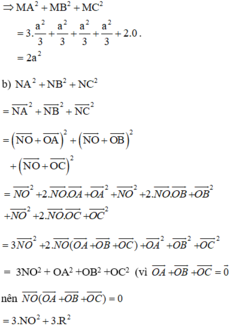
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
CM
8 tháng 9 2017
Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
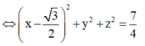
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2
2 tháng 3 2021
a, Gọi I là trọng tâm của ΔABC
⇒ \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
MA2 + MB2 + MC2 = k2
⇔ 3MI2 + 2\(\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+AB^2+AC^2+BC^2\) = k2
⇔ 3MI2 = k2 - 1014
⇔ MI = \(\sqrt{\dfrac{k-1014}{3}}\) = const
Vậy M thuộc \(\left(I;\sqrt{\dfrac{k-1014}{3}}\right)\)
CM
25 tháng 8 2018
Chọn A
Gọi là trọng tâm tam giác ABC. Suy ra: G(2;-2;2)
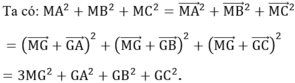
Do tổng GA2 + GB2 + GC2 không đổi nên MA2 + MB2 + MC2 đạt giá trị nhỏ nhất khi và chỉ khi GM2 nhỏ nhất
Mà S nằm trên mặt phẳng (Oyz) nên M là hình chiếu vuông góc của G lên mặt phẳng (Oyz). Suy ra: M(0;-2;2)
Vậy P = x+y+z = 0 + (-2) + 2 = 0
KV
24 tháng 12 2023
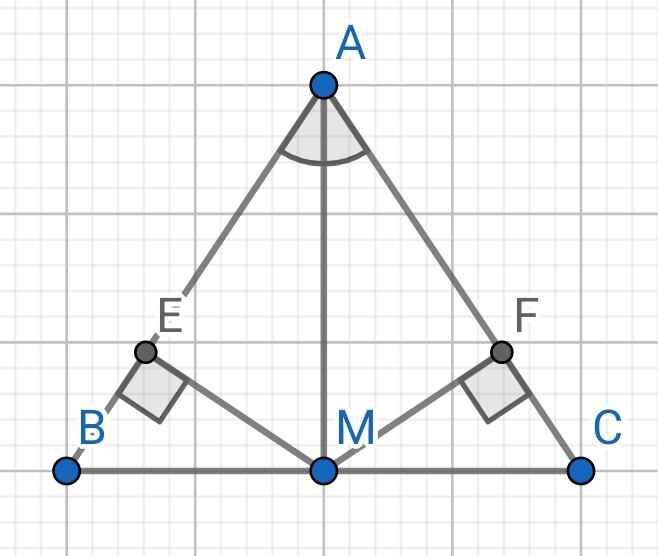a) Do AM là tia phân giác của ∠BAC (gt)
⇒ ∠BAM = ∠CAM
Xét ∆ABM và ∆ACM có:
AB = AC (gt)
∠BAM = ∠CAM (cmt)
AM là cạnh chung
⇒ ∆ABM = ∆ACM (c-g-c)
b) Do ∆ABM = ∆ACM (cmt)
⇒ BM = CM (hai cạnh tương ứng)
⇒ M là trung điểm của BC
Do ∆ABM = ∆ACM (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∠BAM = ∠CAM (cmt)
⇒ ∠EAM = ∠FAM
Xét hai tam giác vuông: ∆AME và ∆AMF có:
AM là cạnh chung
∠EAM = ∠FAM (cmt)
⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng)
P
24 tháng 12 2023
a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)
b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)
c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)
30 tháng 10 2021
a, Vì \(BC^2=400=256+144=AC^2+AB^2\) nên tam giác ABC vuông tại A
b, Áp dụng HTL: \(AM=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\)
\(BM=\dfrac{AB^2}{BC}=7,2 \left(cm\right)\)
c, Áp dụng HTL: \(AE\cdot AB=AM^2\)
Áp dụng PTG: \(AM^2=AC^2-MC^2\)
Vậy \(AE\cdot AB=AC^2-MC^2\)
d, Áp dụng HTL: \(AE\cdot AB=MB\cdot MC=AM^2\)
\(\left\{{}\begin{matrix}\widehat{EAM}=\widehat{ACM}\left(cùng.phụ.\widehat{MAC}\right)\\\widehat{AEM}=\widehat{AMC}=90^0\end{matrix}\right.\Rightarrow\Delta AEM\sim\Delta CMA\left(g.g\right)\\ \Rightarrow EM\cdot AC=AM^2\)
Vậy ta được đpcm
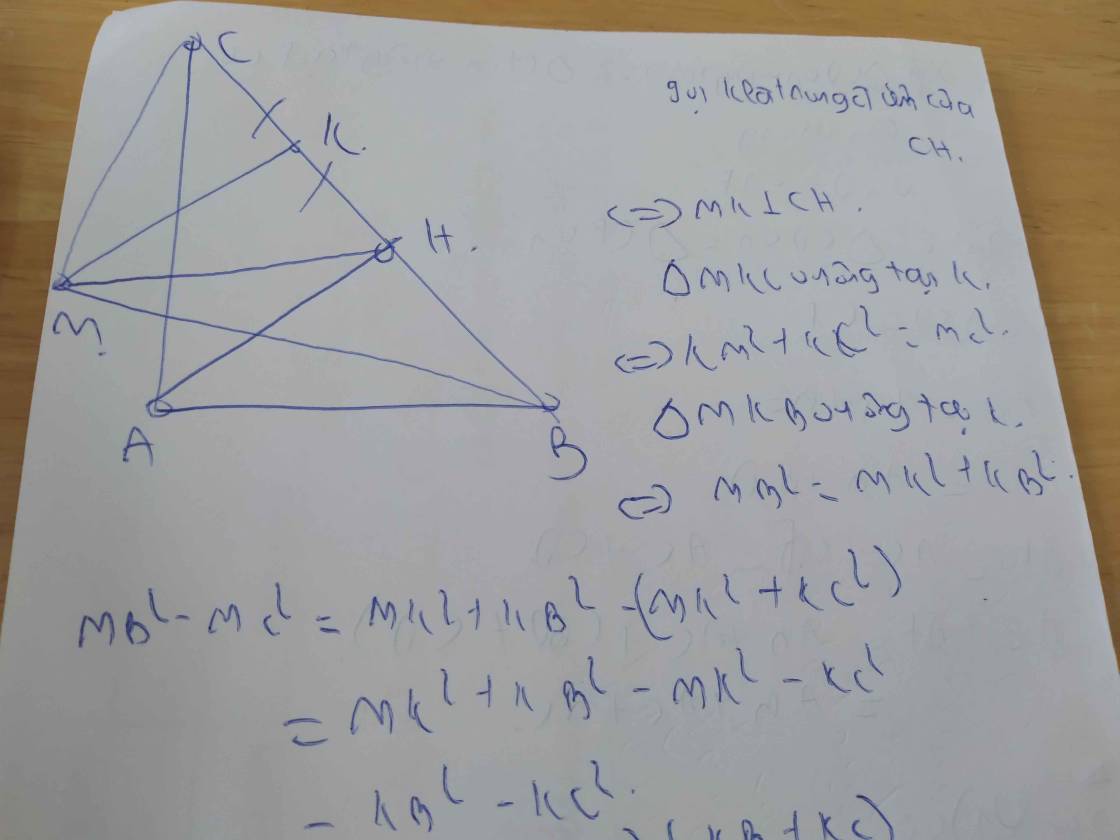
H là điểm như thế nào vậy bạn?