K
Khách
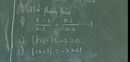
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Giải phương trình 2-x/2009-1=1-x/2010-x/2011
P/S: Ai giúp tôi dc bài toán này cái ạ. Tôi đang cần gấp
4
18 tháng 2 2017
A=|x - 2009| + |x - 2010| + |x - 2011|
*TH1: Xét x ≤ 2009 ; khi đó
. A = 2009 - x + 2010 - x + 2011 -x
. A = 6030 - 3x
có x ≤ 2009 --> -x ≥ -2009 --> -3x ≥ -6027 --> 6030 - 3x ≥ 3
Dấu " = " <=> x = 2009
--> Amin = 3 <=> x = 2009
*TH2 : Xét 2009 < x ≤ 2010 ; ta có
. A = x - 2009 + 2010 - x + 2011 - x
. A = 2012 - x
có x ≤ 2010 --> -x ≥ -2010 --> 2012 - x ≥ 2
--> Amin = 2 <=> x = 2010
*TH3 : Xét 2010 < x < 2011 ; ta có :
. A = x - 2009 + x - 2010 + 2011 - x
. A = x - 8 > 2010 - 8 = 2002 --> không có min
*TH4 : Xét x ≥ 2011 ; ta có :
. A = x - 2009 + x - 2010 + x - 2011
. A = 3x - 6030 ≥ 3.1011 - 6030 = 3
Dấu " = " <=> xảy ra <=> x = 2011
--> Amin = 3 <=> x = 2011
** Kết hợp các trường hợp trên lại ta có :
Amin = 2 <=> x = 2010
HT
1
VP
22 tháng 5 2018
\(4\sqrt{2}x^2-6x-\sqrt{2}=0\) \(0\)
\(\left(a=4\sqrt{2};b=-6;b'=-3;c=-\sqrt{2}\right)\)
\(\Delta'=b'^2-ac\)
\(=\left(-3\right)^2-4.\left(-\sqrt{2}\right)\)
\(=9+4\sqrt{2}\)
\(\sqrt{\Delta}=\sqrt{9+4\sqrt{2}}\)
Vay : phương trình có 2 nghiệp phân biệt
\(x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{3+\sqrt{9+4\sqrt{2}}}{4\sqrt{2}}\)
\(x_2=\frac{-b'-\sqrt{\Delta'}}{a}=\frac{3-\sqrt{9+4\sqrt{2}}}{4\sqrt{2}}\)
21 tháng 5 2018
Khi \(x< -5\) thì\(|x+5|=-x-5\)
\(\Leftrightarrow-x-5=2x-18\)
\(\Leftrightarrow-3x=-13\)
\(\Leftrightarrow x=\frac{13}{3}\)(KTMĐK)
Khi \(x\ge-5\)thì \(|x+5|=x+5\)
\(\Leftrightarrow x+5=2x-18\)
\(\Leftrightarrow-x=-23\)
\(\Leftrightarrow x=23\)(TMĐK)
Vậy:\(S=\left\{23\right\}\)
3 tháng 3 2022
\(\dfrac{x^2+2}{x^2+4}=0\\ \Leftrightarrow x^2+2=0\)
Ta có: \(x^2\ge0;2>0\Rightarrow x^2+2>0\)
Vậy pt vô nghiệm
12 tháng 4 2022
\(\dfrac{1}{a}-\dfrac{a-4}{4a}=6\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\dfrac{4-\left(a-4\right)}{4a}=\dfrac{24a}{4a}\)
\(\Leftrightarrow4-\left(a-4\right)=24a\)
\(\Leftrightarrow4-a+4=24a\)
\(\Leftrightarrow8=25a\)
\(\Leftrightarrow a=\dfrac{8}{25}\left(tm\right)\)
Vậy \(S=\left\{\dfrac{8}{25}\right\}\)
14 tháng 3 2022
Ta có:
(2 - 3x)(x + 8) = (3x - 2)(3 - 5x)
⇔ (2 - 3x)(x + 8) - (3x - 2)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8) + (2 - 3x)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8 + 3 - 5x) = 0
⇔ (2 - 3x)(11 - 4x) = 0
⇔ 2 - 3x = 0 hay 11 - 4x = 0
⇔ 2 = 3x hay 11 = 4x
⇔ x = \(\dfrac{2}{3}\) hay x = \(\dfrac{11}{4}\)
Vậy tập nghiệm của pt S = \(\left\{\dfrac{2}{3};\dfrac{11}{4}\right\}\)
14 tháng 3 2022
<=> (2-3x ) (x+8) + (2-3x ) (3-5x)=0
<=> (2-3x ) ( x+8 + 3-5x ) =0
<=> (2-3x ) ( 11 - 4x ) = 0
=> 2-3x =0 hoặc 11-4x =0
3x = 2 4x =11
x = 2/3 x = 11/4
NT
3
NM
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2023
\(\Leftrightarrow2cos4x\left(cos2x-sin2x\right)=0\)
\(\Leftrightarrow cos4x=0\) (do \(cos4x=cos^22x-sin^22x\) đã bao hàm \(cos2x-sin2x\))
\(\Rightarrow4x=\dfrac{\pi}{2}+k\pi\)
\(\Rightarrow x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\)
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
\(\Leftrightarrow2sin^3x+1-sin^2x-1=0\)
\(\Leftrightarrow sin^2x\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
a, \(\frac{x-3}{x-2}+\frac{x-2}{x-4}=-1\left(đk:x\ne2;4\right)\)
\(< =>\frac{\left(x-3\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}+\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x-4\right)}=-\frac{\left(x-2\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}\)
\(=>x^2-7x+12+x^2-4x+4=-\left(x^2-6x+8\right)\)
\(< =>2x^2-11x+16+x^2-6x+8=0\)
\(< =>3x^2-17x+24=0\)
\(< =>3x^2-9x-8x+24=0\)
\(< =>3x\left(x-3\right)-8\left(x-3\right)=0\)
\(< =>\left(x-3\right)\left(3x-8\right)=0\)
\(< =>\orbr{\begin{cases}x=3\\x=\frac{8}{3}\end{cases}}\)(thỏa mãn)
b, \(|5x|-3x-2=0\)
Với \(x\ge0\)thì \(PT< =>5x-3x-2=0\)
\(< =>2x-2=0< =>x=1\)(tm)
Với\(x< 0\)thì \(PT< =>-5x-3x-2=0\)
\(< =>x=\frac{2}{8}=\frac{1}{4}\)(loại)
Vậy ...