- giúp tớ tớ cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số hoa 7A,7B,7C ll là \(a,b,c(a,b,c\in \mathbb{N^*})\)
Áp dụng tc dtsbn:
\(\dfrac{a}{12}=\dfrac{b}{10}=\dfrac{c}{9}=\dfrac{b+c-a}{10+9-12}=\dfrac{140}{7}=20\\ \Rightarrow\left\{{}\begin{matrix}a=240\\b=200\\c=180\end{matrix}\right.\)
Vậy ...

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{15}=\dfrac{b}{17}=\dfrac{c}{16}=\dfrac{b+c-a}{17+16-15}=\dfrac{270}{18}=15\)
Do đó: a=225; b=255; c=240

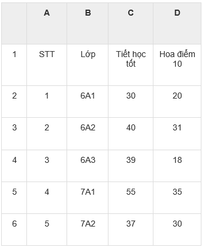
a) = SUM(C2:C6)
b) = SUM(D2:D6)
c) = MAX(C2:C6)
d) = MIN(D2:D6)

Gọi 3 tổ có số học sinh lần lượt là: a, b, c ( \(a,b,c\inℕ^∗;a,b,c< 135\))
Theo bài ra, ta có: \(a+b+c=135\)và \(a:b:c=4:5:6\)
Từ \(a:b:c=4:5:6\)\(\Rightarrow\frac{a}{4}=\frac{b}{5}=\frac{c}{6}=\frac{a+b+c}{4+5+6}=\frac{135}{15}=9\)
\(\Rightarrow a=9.4=36\); \(b=9.5=45\); \(c=9.6=54\)
Vậy số bông hoa của mỗi tổ lần lượt là 36 , 45 , 54
Gọi số bông hoa điểm tốt của tổ 1 là \(x\) ( 700 ≤ \(x\) < 800; \(x\) \(\in\) N)
Vì số bông hoa điểm tốt của tổ 1 là bội của 4; 7; 9 nên số bông hoa điểm tốt của tổ 1 thuộc bội chung của 4; 7; 9 ⇒ \(x\in\) BC(4; 7;9)
4 = 22; 7 = 7; 9 = 32
BCNN(4; 7; 9) = 22.32.7 = 252
\(x\in\) BC(4; 7;9) = {0; 252; 756; 808;...;}
Vì 700 ≤ \(x\) < 800 nên \(x\) = 756
Kết luận: số bông hoa điểm tốt của tổ 1 lớp 6A là 756 bông hoa.