giải giúp mình nhanh nhé ! theo cách giải của lớp 9 nhen ><
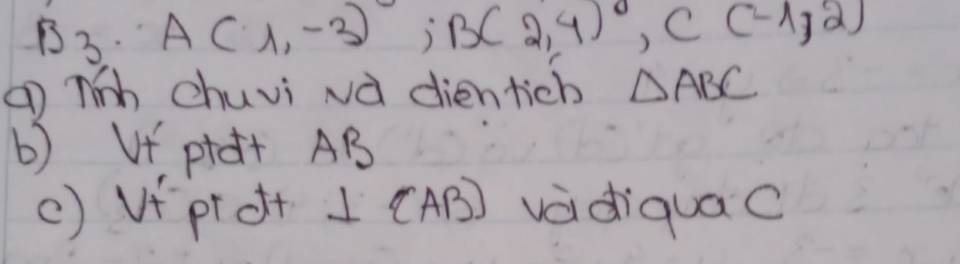
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E


a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

37.37 x 5959.59 = 222709.8783
59.59 x 3737.37 = 222709.8783
Vậy: điền dấu = nhé!

Ta có :
155 : b = a (dư 12)
=> 155 = ab + 12 => a.b = 155 - 12 = 143 = 11.13 = 13.11
Vì b > 12 => b = 13; a = 11
Vậy số chia bằng 13; thương bằng 11
Gọi số chia và thương lần lượt là b , q ( b > 12 ; b , q \(\in\) N )
Theo phép chia có dư thì ta có :
=> a = b . q + r
=> a - r = b . q
=> 155 - 12 = b . q
=> 143 = b . q
Lại có : 143 = 11 . 13 = 13 . 11
Mà b > 12
=> b = 13 và q = 11
Vậy số chia là 13 và thương bằng 11

Câu 1
Gọi số đầu là a (a lẻ)
=> 2số còn lại là:
(a+2) và (a+4) ( vì 2 số lẻ liên tiếp cách nhau hai đơn vị)
Ta có:
a(a+2)(a+4)=105
Nhân đa thức, chuyển vế ta được:
a^3+6a^2+8a-105=0
=> a^3-3a^2+9a^2-27a+35a-105=0
=> a^2(a-3)+9a(a-3)+35(a-3)=0
=> (a^2+9a+35)(a-3)=0
Vì a>0(a lẻ) => (a-3)=0
=>a=3
vậy 2 số còn lại là 5và 7
3 số đó là 3,5,7
Câu 2
Gọi 4 số đó là x,x+2,x+4,x+6
Ta có x+x+2+x+4+X+6=156
Nên X x 4 +2=156
X=(156-12):4=36
Vậy 4 số đó là 36,38,40,42
Câu 1
Gọi số đầu là a (a lẻ)
=> 2số còn lại là:
(a+2) và (a+4) ( vì 2 số lẻ liên tiếp cách nhau hai đơn vị)
Ta có:
a(a+2)(a+4)=105
Nhân đa thức, chuyển vế ta được:
a^3+6a^2+8a-105=0
=> a^3-3a^2+9a^2-27a+35a-105=0
=> a^2(a-3)+9a(a-3)+35(a-3)=0
=> (a^2+9a+35)(a-3)=0
Vì a>0(a lẻ) => (a-3)=0
=>a=3
vậy 2 số còn lại là 5và 7
3 số đó là 3,5,7
Câu 2
Gọi 4 số đó là x,x+2,x+4,x+6
Ta có x+x+2+x+4+X+6=156
Nên X x 4 +2=156
X=(156-12):4=36
Vậy 4 số đó là 36,38,40,42
a: A(1;-3); B(2;4); C(-1;2)
\(AB=\sqrt{\left(2-1\right)^2+\left(4+3\right)^2}=5\sqrt{2}\)
\(BC=\sqrt{\left(-1-2\right)^2+\left(2-4\right)^2}=\sqrt{13}\)
\(AC=\sqrt{\left(-1-1\right)^2+\left(2+3\right)^2}=\sqrt{29}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=5\sqrt{2}+\sqrt{13}+\sqrt{29}\)
Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{50+29-13}{2\cdot5\sqrt{2}\cdot\sqrt{29}}=\dfrac{33}{5\sqrt{58}}\)
\(sin^2A+cos^2A=1\)
=>\(sin^2A=1-\left(\dfrac{33}{5\sqrt{58}}\right)^2=\dfrac{361}{1450}\)
=>\(sinA=\sqrt{\dfrac{361}{1450}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{\dfrac{361}{1450}\cdot50\cdot29}=\dfrac{19}{2}\)
b: Gọi (d): y=ax+b là phương trình đường thẳng AB
(d) đi qua A(1;-3) và B(2;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-3\\2a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a=-7\\a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-3-a=-3-7=-10\end{matrix}\right.\)
Vậy: (d): y=7x-10
c: Gọi (d1):y=ax+b là phương trình đường thẳng cần tìm
Vì (d1) vuông góc AB nên \(a\cdot7=-1\)
=>\(a=-\dfrac{1}{7}\)
=>(d1): \(y=-\dfrac{1}{7}x+b\)
Thay x=-1 và y=2 vào (d1), ta được:
\(b+\dfrac{1}{7}=2\)
=>\(b=2-\dfrac{1}{7}=\dfrac{13}{7}\)
Vậy: (d1): \(y=-\dfrac{1}{7}x+\dfrac{13}{7}\)