giúp em với ạ em cần nộp bàii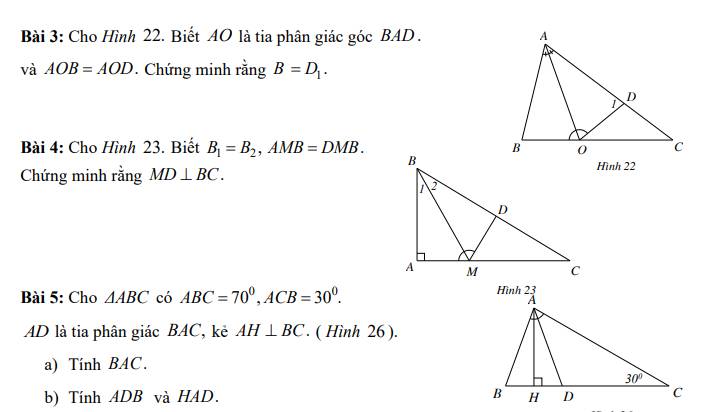
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2
a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

xét tứ giác ANMP có
góc NAP = 90 độ ( AB vuông góc AC)
góc MPA = 90 độ (MP vuông góc AC)
Góc ANM = 90 độ (MN vuông góc AB)
=> tứ giác AMNP là hình chữ nhật

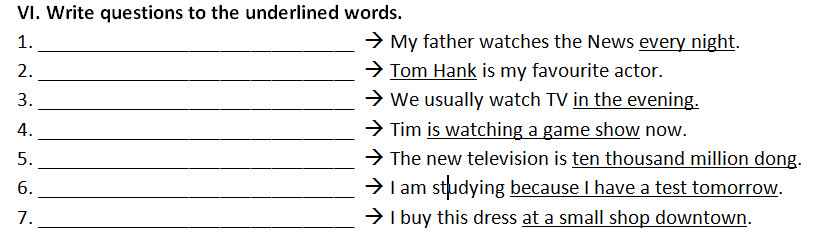
How often does your father watch the News?
Who is your favorite actor?
When do you usually watch TV?
What is Tim doing?
How much does the new television cost?
Why are you studying?
Where do you buy this dress?
1.How often does your father watch the News?
2.Who is your favorite actor?
3.When do you usually watch TV?
4.What is Tim doing?
5.How much does the new television cost?
6.Why are you studying?
7.Where do you buy this dress?

bạn có thể cho mình cái đề được không máy của mình nó hay bị mờ ảnh á


1a.
$x^2-5x+6=x^2-2x-(3x-6)=x(x-2)-3(x-2)=(x-2)(x-3)$
1b.
$3x^2+9x-30=3(x^2+3x-10)=3(x^2-2x+5x-10)$
$=3[x(x-2)+5(x-2)]=3(x-2)(x+5)$
1c.
$x^2-3x+2=(x^2-x)-(2x-2)=x(x-1)-2(x-1)=(x-1)(x-2)$
1d.
$x^2-9x+18=x^2-3x-(6x-18)=x(x-3)-6(x-3)=(x-3)(x-6)$
1e.
$x^2-6x+8=x^2-2x-(4x-8)=x(x-2)-4(x-2)=(x-2)(x-4)$
1f.
$x^2-5x-14=x^2-7x+2x-14=x(x-7)+2(x-7)=(x+2)(x-7)$
1g.
$x^2+6x+5=(x^2+x)+(5x+5)=x(x+1)+5(x+1)=(x+1)(x+5)$
1h.
$x^2-7x+12=x^2-3x-(4x-12)=x(x-3)-4(x-3)=(x-3)(x-4)$
1i.
$x^2-7x+10=(x^2-2x)-(5x-10)=x(x-2)-5(x-2)=(x-2)(x-5)$

\(1,\left\{{}\begin{matrix}3x-y=5\\5x+2y=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+2\left(3x-5\right)=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\5x+6x-10=23\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3x-5\\11x=33\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=3.3-5\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
\(2,\left\{{}\begin{matrix}5x-4y=3\\2x+y=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-4\left(4-2x\right)=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}5x-16+8x=3\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}13x=19\\y=4-2x\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=4-2.\dfrac{19}{13}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{13}\\y=\dfrac{14}{13}\end{matrix}\right.\)











3:
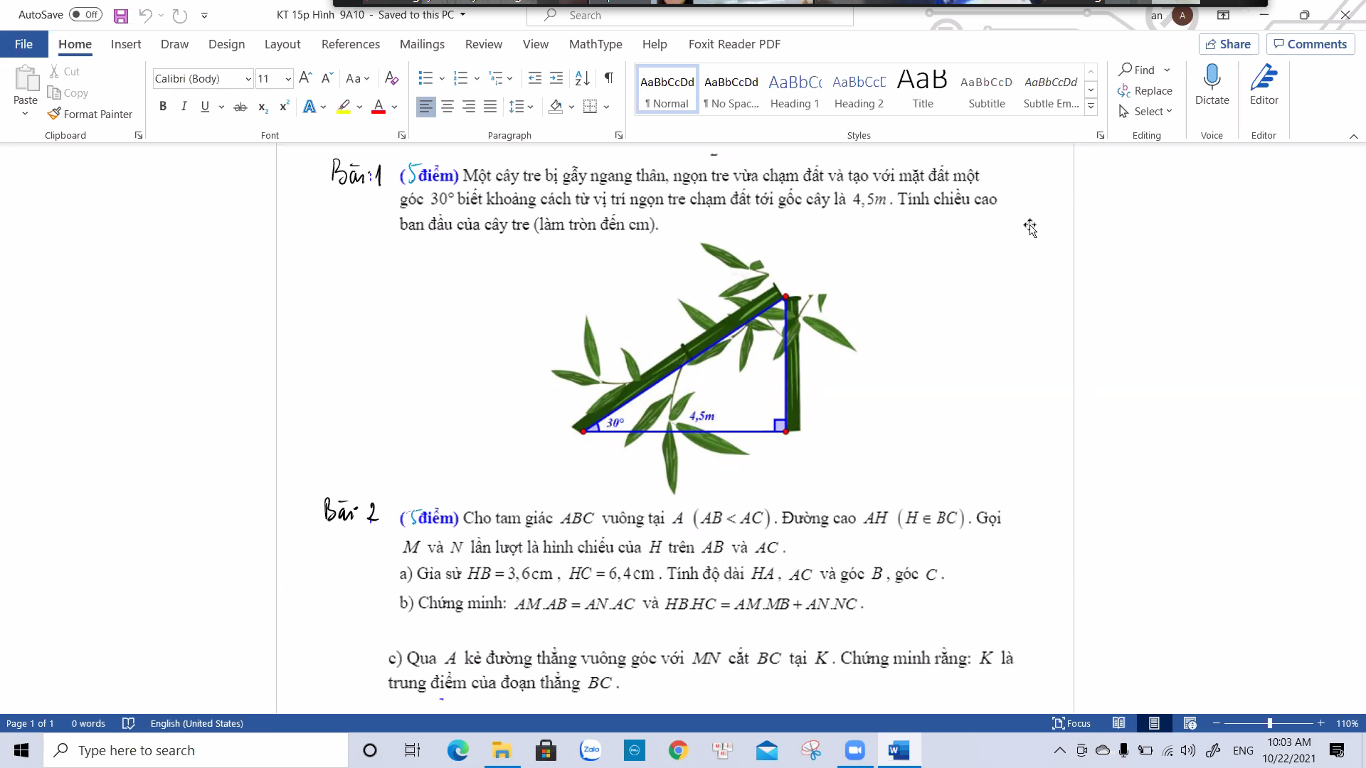
Xét ΔABO và ΔADO có
\(\widehat{AOB}=\widehat{AOD}\)
OA chung
\(\widehat{BAO}=\widehat{DAO}\)
Do đó: ΔABO=ΔADO
=>\(\widehat{ABO}=\widehat{ADO}\)(ĐPCM)
Bài 4:
Xét ΔBAM và ΔBDM có
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
\(\widehat{AMB}=\widehat{DMB}\)
Do đó: ΔBAM=ΔBDM
=>\(\widehat{BAM}=\widehat{BDM}=90^0\)
=>DM\(\perp\)BC
5:
a: Xét ΔBAC có
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=180^0-70^0-30^0=80^0\)
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{80^0}{2}=40^0\)
Xét ΔADC có góc ADB là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{C}=40^0+30^0=70^0\)
ΔAHD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}=90^0-70^0=20^0\)