Một vật nhỏ thực hiện dao động điều hòa với phương trình \(x=5\cos\left(4\pi t-\dfrac{\pi}{3}\right)\left(cm\right)\). Tại thời điểm t1, vật có li độ \(2,5\sqrt{2}\left(cm\right)\) và đang có xu hướng giảm. Li độ của vật sau thời điểm đó \(\dfrac{7}{48}\left(s\right)\) là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 9 2023
\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3
20 tháng 8 2023
2:
\(x=-3\cdot cos\left(2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(pi+2pi\cdot t+pi\right)\)
\(=3\cdot cos\left(2pi\cdot t+2pi\right)\)
Biên độ là A=3
Tần số góc là 2pi
Chu kì là T=2pi/2pi=1
Pha ban đầu là 2pi
Pha của dao động tại thời điểm t=0,5 giây là;
\(2pi\cdot0.5+2pi=3pi\)
30 tháng 9
bài 1:
Biên độ góc: A = 5 cm
Tần số góc = 10 pi
Chu kì T = 2pi / tần số góc = 0,2 s
pha dao động là 10 pi x 1 - pi /2 = 19/ 2 pi
HT
23 tháng 7 2021
Đối với những bài tìm quãng đường trong khoảng từ t1 đến t2 thì bạn lấy t2-t1 rồi phân tích chúng ra thành \(\left[{}\begin{matrix}t_2-t_1=n.\dfrac{T}{2}+t'\\t_2-t_1=n.T+t''\end{matrix}\right.\) để dễ dàng tính. Tuyệt đối ko được phân tích thành T/4 hay T/3; T/6;T/v.v. bởi nó ko luôn đúng trong các trường hợp, nếu bạn cần mình sẽ lấy ví dụ cụ thể. Giờ mình sẽ áp dụng vô bài của bạn
\(t_2-t_1=\dfrac{17}{3}-2=\dfrac{11}{3}\left(s\right)=3+\dfrac{2}{3}\)
\(T=\dfrac{2\pi}{\pi}=2s\Rightarrow t_2-t_1=3.\dfrac{T}{2}+\dfrac{2}{3}\)
Trong 3T/2 vật đi được quãng đường là: \(S_1=6A=30\left(cm\right)\)
Tại thời điểm t1=2s, lúc này vật đã quay được:\(\varphi=2\pi\left(rad\right)\) nghĩa là quay về vị trí ban đầu
Trong 2/3 s vật quay được góc: \(\varphi=\dfrac{2}{3}\pi\left(rad\right)\)
Sử dụng đường tròn lượng giác, vật ở vị trí có pha là 2pi/3, quay được góc 2pi/3 thì lúc này vật có li độ là: \(x=-2,5\left(cm\right)\)
Nghĩa là vật đi từ vị trí có li độ x1=-2,5 theo chiều âm đến vị trí có li độ x2=-2,5 theo chiều dương, vậy quãng đường vật đi được là: \(S_2=\dfrac{A}{2}+\dfrac{A}{2}=A=5\left(cm\right)\)
Vậy tổng quãng đường vật đi được là: \(S=S_1+S_2=35\left(cm\right)\)
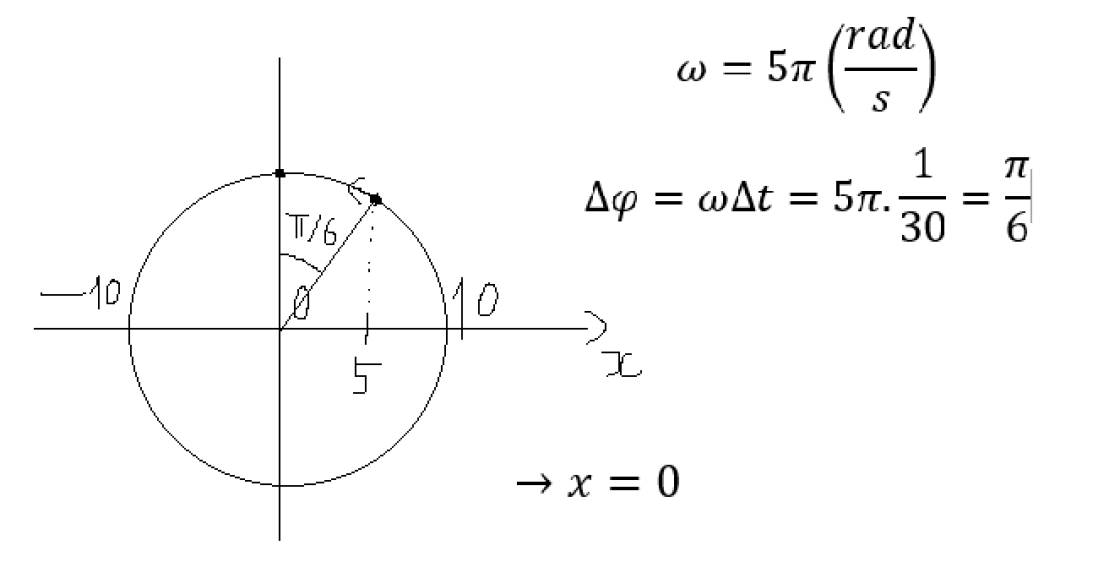
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)
Hình vẽ đây nha