Giúp e vs ặ:(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

23 tháng 12 2021
\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{12^2}{6}=24\Omega\)
\(R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{20\cdot20}{20+20}=10\Omega\)
\(R_{tđ}=R_Đ+R_{12}=24+10=34\Omega\)
\(I_A=I_m=\dfrac{U_m}{R_{tđ}}=\dfrac{15}{34}=0,44A\)

9 tháng 10 2021
\(\dfrac{x+1}{3}=\dfrac{y+2}{4}=\dfrac{z+3}{5}\\ =\dfrac{x+1+y+2+z+3}{3+4+5}=\dfrac{24}{12}=2\)
Từ:
\(\dfrac{x+1}{3}=2\\ =>x+1=6\\ < =>x=5\)
\(\dfrac{y+2}{4}=2\\ =>y+2=8\\ < =>y=6\)
\(z=18-x-y=18-5-6=7\)
HA
3


H
26 tháng 10 2021
$(1) 4Al + 3O_2 \xrightarrow{t^o} 2Al_2O_3$
$(2) Al_2O_3 + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2O$
$(3) Al_2(SO_4)_3 + 6NaOH \to 2Al(OH)_3 + 3Na_2SO_4$
H
4

LT
0


H
3

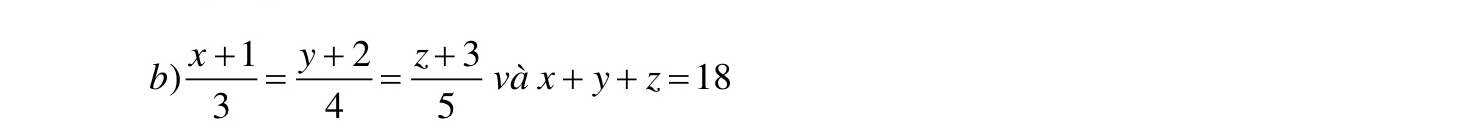

 Lm giúp mik câu 8 vs ặ mik đng cần gấp
Lm giúp mik câu 8 vs ặ mik đng cần gấp
1, đoạn trích trên kể lại trận đánh ở đồi Hà Hồi Và Ngọc Hồi
-Nửa đêm mồng 3 tháng giêng đánh đồn Hà Hồi
-Mờ sáng mồng 5 đánh đồn Ngọc Hồi
2,BPNT:Nói quá
Tác dụng: Ý muốn nói giặc chết rất nhiều không thể đếm được
3,Tự viết
4, Tác giả:Lý Thường Kiệt
Tác phẩm:Nam Quốc sơn hà