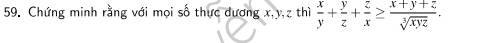cmr với số thức dương x y z thì x/y+y/z+z/x >=(x+y+z)/căn 3 của xyz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
KT
0

HD
2

25 tháng 3 2018
Ta có: \(xy+yz+zx>\frac{18xyz}{2+xyz}\)
\(\Leftrightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{18}{2+xyz}\)Vì \(x;y;z>0\)
Áp dụng BĐT Cauchy-Schwazt,ta có:
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{9}{x+y+z}=9=\frac{18}{2}\)
Mà \(x;y;z>0\Rightarrow\frac{18}{2}>\frac{18}{2+xyz}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{18}{2+xyz}\Leftrightarrow xy+yz+zx>\frac{18yz}{2+xyz}\left(đpcm\right)\)
Q
0

QK
0

câu hỏi đây nhé