số học sinh khối 6 của một trường trong khoảng từ 500 đến 600 khi xep hang 5;9;12thua ra 2 hoc sinh tinh so hoc sinh cua truong do
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


trước hết ta đi tìm BCNN của 12; 15;18 là 180
vậy số hs khôi 6 lả 180 x 3 = 540 hs
( dạng toán này mk gặp trong violympic hoài)
Số học sinh của khối 6 là bội chung của 12; 15 và 18
12 = 22.3; 15 = 3.5; 18 = 32.2
BCNN(12; 15; 18) = 22.32.5 = 180
(Rightarrow BC(12; 15; 18) = left{{0; 180; 360; 540; 720; …}right})
Trong các số thuộc BC(12; 15; 18) chỉ có số 540 là trong khoảng từ 500 đến 600
Vậy số học sinh khối 6 của trường đó là 540 học sinh

Giải thích các bước giải:
Gọi số học sinh của khối sáu là a(với a thuộc N*) ta có:
theo bài ra ta có:
a-5 chia hết cho 12
a-5 chia hết cho 15
a-5 chia hết cho 18
=> a-5 thuộc bội chung của (12,15,18)
Mà bội chung của 12, 15 ,18 = {0,180,360,540,....}
Mà a>500, a<600 => a-5 = 540
=> a = 540 + 5 = 545

Gọi số học sinh trường đó là a:
Điều kiện :
a : 10 dư 2
a : 12 dư 2
a : 18 dư 2
Vậy a - 2 chia hết cho 10,12,18 .. a-2 thuộc BC(10,12,18)
Ta có :
10 = 2.5
12 = 22.3
18 = 2.32
BCNN(10,12,18) = 22. 32.5 = 180
BC(10,12,18) = B(180) = {0;180;360; 540;720}
Mà 500< a <600
=> a - 2 = 540
=> a = 542
Vậy số học sinh trường đó là 542
Đ/s: 542 học sinh
Gọi số học sinh trường đó là x (học sinh) ; (500 \(\le x\le600;x\inℕ^∗\))
Ta có : \(\hept{\begin{cases}x:12\text{ dư 2}\\x:10\text{ dư 2}\\x:18\text{ dư 2}\end{cases}\Rightarrow\hept{\begin{cases}x-2⋮12\\x-2⋮10\\x-2⋮18\end{cases}}}\Rightarrow x-2\in BC\left(12;10;18\right)\)
Phân tích ra thừa số nguyên tố ta được :
12 = 3.22
10 = 2.5
18 = 32.2
=> BCNN(12;10;18) = 22.32.5 = 180
=> \(x-2\in B\left(180\right)\)
=> \(x-2\in\left\{0;180;360;540;720\right\}\)
=> \(x\in\left\{2;182;362;542;722;...\right\}\)
Kết hợp điều kiện => x = 542
Vậy trường đó có 542 học sinh

Gọi a là số học sinh cần tìm (a thuộc N sao)
Theo đề bài ta có: a thuộc BC(12;15;18)
12=22x3; 15=3x5; 18=2x32
BCNN(12;15;18)=22x32x5=180
BC(12;15;18)=B(12;15;18)={0;180;360;540;720;...)
Vì số học sinh nằm trong khoảng từ 500 đến 600 nên :
ta chọn a=540
Vậy số học sinh khối 6 có 540 (học sinh)
Ta gọi : A là số học sinh khối 6 của trường .
Vì : A chia hết cho 12 , 15 , 18 , 500 nhỏ hơn hoặc bằng A và 600 lớn hơn hoặc bằng A ( Ở đây mình dùng chữ nhưng bạn nên dùng kí hiệu toán học sẽ đúng hơn )
-> A thuộc BC { 12 , 15 , 18 }
12 = 2^2 . 3
15 = 3 . 5
18 = 2 . 3^2
BCNN { 12 , 15 , 18 } = 2^2 . 3^2 . 5 = 180 .
BC { 12 , 15 , 18 } = BC { 180 } = { 0 , 180 , 360 , 540 , ... }
Mà : 500 nhỏ hơn hoặc bằng A và 600 lớn hơn hoặc bằng A .
-> A = 540 .
Vậy : Số học sinh khối 6 của trường là 540 học sinh .

Số học sinh khối 6 của trường đó sẽ là bội của 12,15,18 từ khoảng 500 đến 600
B12=504;516;528;540;.......600
B15=510;525;540;.....600
B18=504;522;540.....600
BCNN của 3 số là 540 và số học sinh khối 6 của trường là 500 đến 600
Vậy số học sinh khối 6 của trường đó là 540 học sinh

Gọi số học sinh của trường đó là xx (hs); ( 1600≤x≤20001600≤x≤2000)
Vì số hs khi xếp hàng 3, hàng 4, hàng 7, hàng 9 đều vừa đủ nên x∈BC(3,4,7,9)x∈BC(3,4,7,9)
Ta có :
3=33=3
4=224=22
7=77=7
9=329=32
⇒BCNN(3,4,7,9)=32.22.7=252⇒BCNN(3,4,7,9)=32.22.7=252
⇒BCNN(3,4,7,9)=BC(3,4,7,9)⇒BCNN(3,4,7,9)=BC(3,4,7,9) ={252;504;756;1008;1260;1512;1764;2016;..}={252;504;756;1008;1260;1512;1764;2016;..}
mà 1600≤x≤20001600≤x≤2000 ⇒x=1764⇒x=1764 hs
Vậy số hs của trường đó là 17641764 hs
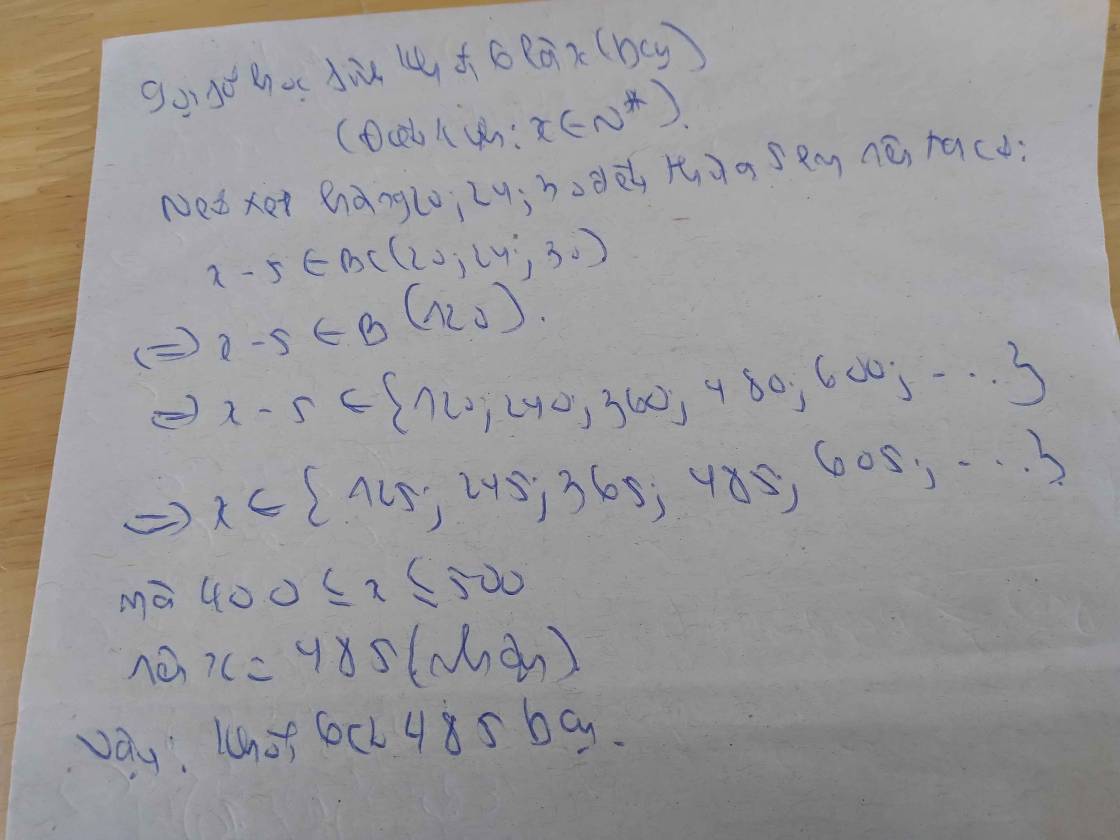
Gọi \(x\) (học sinh) là số học sinh cần tìm \(\left(x\in N,500< x< 600\right)\)
Do khi xếp hàng 5; 9; 12 đều thừa 2
\(\Rightarrow x-2\in BC\left(5;9;12\right)\)
Ta có:
\(5=5\)
\(9=3^2\)
\(12=2^2.3\)
\(\Rightarrow BCNN\left(5;9;12\right)=2^2.3^2.5=180\)
\(\Rightarrow x-2\in BC\left(5;9;12\right)=B\left(180\right)=\left\{0;180;360;540;720;...\right\}\)
\(\Rightarrow x\in\left\{2;182;362;542;722;...\right\}\)
Mà \(500< x< 600\Rightarrow x=542\)
Vậy số học sinh cần tìm là 542 học sinh