Cho hình thoi ABCD ; AC cắt BD tại O qua B kẻ Bx //AC , qua C kẻ Cy // BD , Bx cắt Cy tại K
a) Tứ giác BOCK là hình gì ? vì sao ?
b) CM : OK=AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
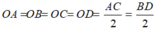
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

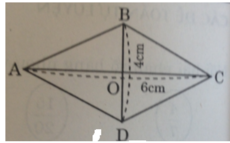
A B C D O AC = 8 BD = 6
Gọi \(O\) là giao điểm của \(AC\)và \(BD\).
Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)
Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)
Áp dụng định lí Pitago trong \(\Delta AOB\) có:
\(AB^2=AO^2+OB^2\)
\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)
\(\Rightarrow AB=5cm\)
\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)
Vậy ...............

\(AB=\dfrac{BH}{\sin A}=\dfrac{1,5}{\sin30^0}=3\left(cm\right)\)
Do đó \(P_{ABCD}=4AB=12\left(cm\right)\)
a) Tứ giác BOCK là tứ giác cân.
Để chứng minh điều này, ta cần chứng minh hai cặp góc của tứ giác BOCK bằng nhau.
Góc BOC và góc BKC là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau:
Góc BOC = Góc BKC. Góc BCO và góc BCK là hai góc đối nhau nằm ở cùng một cạnh BC, nên chúng bằng nhau: Góc BCO = Góc BCK.
Vì vậy, tứ giác BOCK có hai cặp góc bằng nhau, tức là tứ giác BOCK là tứ giác cân.
b) Ta cần chứng minh CM : OK = AD.
Vì tứ giác BOCK là tứ giác cân, nên ta có BC = BK.
Do đó, tam giác BCK là tam giác cân, nên ta có CM là đường trung tuyến của tam giác BCK.
Vì vậy, ta có CM = MK.
Từ đó, ta có CM : OK = MK : OK = 1 : 1 = 1.Tuy nhiên, để chứng minh CM : OK = AD, ta cần thêm thông tin về mối quan hệ giữa các đoạn thẳng trong hình thoi ABCD.