bài 4 cho tam giác ABC vuông tại A(AB>AC)đường cao AH.Từ H kể HNvuông AC,HMvuôngAB(thuộc AC,Mthuộc AB).Trên tia đối của tia NH lấy điểm E sao cho NE =NH.
a)tứ giác AMNH là hình gì?Vì sao. b) Chứng minh tứ giác AMNE là hình bình hành. c) gọi O là trung điểm MN và AH,AM cắt AH tại G.Chứng minh AE=OGHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ANDM có
\(\widehat{AND}=\widehat{AMD}=\widehat{MAN}=90^0\)
=>ANDM là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của CB
DN//AB
Do đó: N là trung điểm của AC
Xét tứ giác ADCEcó
N là trung điểm chung của AC và DE
=>ADCE là hình bình hành
Hình bình hành ADCE có AC\(\perp\)DE
nên ADCE là hình thoi
c:
Xét ΔABC có
D là trung điểm của BC
DM//AC
Do đó: M là trung điểm của AB
Để AMDN là hình vuông thì AM=AN
mà \(AM=\dfrac{AB}{2};AN=\dfrac{AC}{2}\)
nên AB=AC

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Xét tứ giác ABKI có
M là trung điểm chung của AK và BI
Do đó: ABKI là hình bình hành
=>KI//AB
mà AB\(\perp\)AC
nên KI\(\perp\)AC
Xét ΔCAI có
IK,CH là đường cao
IK cắt CH tại K
Do đó: K là trực tâm của ΔCAI
=>AK\(\perp\)IC

a: Xét tứ giác ADCH có
M là trung điểm chung của AC và HD
góc AHC=90 độ
Do đó: ADCH là hình chữ nhật
b: Xét tứ giác ADHE có
AD//HE
AD=HE
Do đó: ADHE là hình bình hành

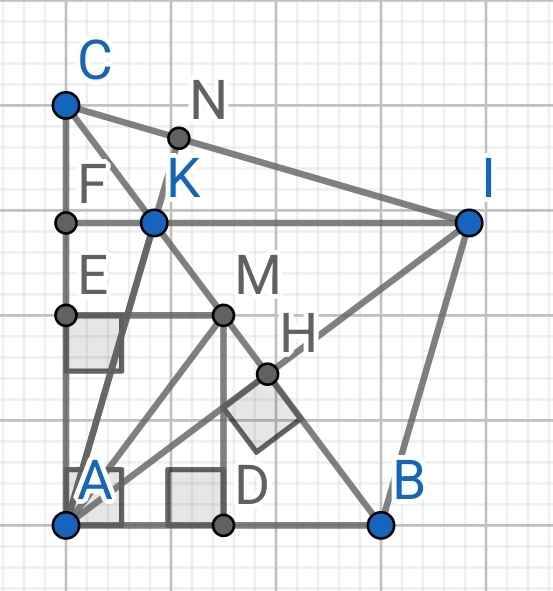
a) Tứ giác ADME có:
∠AEM = ∠ADM = ∠EAD = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do HI = HA (gt)
⇒ H là trung điểm của AI
Do HK = HB (gt)
⇒ H là trung điểm của BK
Tứ giác ABIK có:
H là trung điểm của AI (cmt)
H là trung điểm của BK (cmt)
⇒ ABIK là hình bình hành
⇒ IK // AB
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ IK ⊥ AC
⇒ IK là đường cao của ∆ACI
Lại có:
AH ⊥ BC (do AH là đường cao của ∆ABC)
⇒ CH ⊥ AI
⇒ CH là đường cao thứ hai của ∆ACI
∆ACI có:
IK là đường cao (cmt)
CH là đường cao (cmt)
⇒ AK là đường cao thứ ba của ∆ACI
⇒ AK ⊥ IC

a: Xét tứ giác AHCE có
D là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b: AHCE là hình bình hành
=>AE//CH
mà H\(\in\)CI
nên AE//HI
Xét tứ giác AEHI có
AE//HI
AI//HE
Do đó: AEHI là hình bình hành
c: Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
Ta có: ΔCAK cân tại C
mà CB là đường cao
nên CB là phân giác của \(\widehat{ACK}\)

a) Xét tứ giác EFCB có
EF//BC (gt)
=> EFCB là hình thang
b)
Xét tam giác KHA và tam giác FAE có
KA=AF (gt)
AH=AE(gt)
góc KAH = góc EAF (đđ)
=> tam giác KHA = tam giác FAE ( c-g-c)
=> góc HKA= góc AFE( c-g-t-ư) (1)
mặt khác ta có EF//BC
=> góc AFE = góc ACB ( đồng vị ) (2)
(1)&(2)=> góc HKA = góc ACB
mà chúng ở vị trí so le trong nên KH//BC
xét tức giác KHBC có KH//BC (cmt)
=> KHBC là hình thang

a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
mà góc BAC=90 độ
nên ABDC là hình chữ nhật
b,d: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AFE=góc AHE=góc ABC
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc ACB
=>góc MAC+góc EFA=90 độ
=>AM vuông góc với EF
c: Xét ΔADI có
H,M lần lượt là trung điểm của AI và AD
nên HM là đường trung bình
=>HM//DI
=>DI//BC
Xét ΔCIA có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCIA cân tại C
=>CI=CA=DB
=>BIDC là hình thang cân