2Cho biểu thức 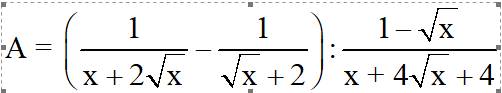
(với x > 0; x ¹ 1)
a) Rút gọn biểu thức A.
GIÚP TỚ VỚI Ạ PLSSSS
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm :
1) Khi x=9 ; giá trị của A là :
\(A=\frac{\sqrt{9}}{\sqrt{9}+2}=\frac{3}{3+2}=\frac{3}{5}\)
2) Ta có :
\(B=...\)
\(=\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x+2}\right)}\)
\(=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}}{\sqrt{x}-2}\)
3) Ta có :
\(\frac{A}{B}=\frac{\sqrt{x}}{\sqrt{x}+2}\div\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}\)
Xét :
\(\frac{A}{B}+1=\frac{4}{\sqrt{x+2}}>0\Rightarrow\frac{A}{B}>-1\)
=> Điều phải chứng minh
1, thay x=9(TMĐKXĐ) vào A ta đk:
A=\(\dfrac{\sqrt{9}}{\sqrt{9}-2}=3\)
vậy khi x=9 thì A =3
2,với x>0,x≠4 ta đk:
B=\(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
vậy B=\(\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
3,\(\dfrac{A}{B}>-1\) (x>0,x≠4)
⇒\(\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}>-1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}>-1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>-1\)
⇒\(\sqrt{x}-2>-1\) (vì \(\sqrt{x}+2>0\))
⇔\(\sqrt{x}>1\)⇔x=1 (TM)
vậy x=1 thì \(\dfrac{A}{B}>-1\) với x>0 và x≠4

Bài 1: \(A=x^2-2x+3\)
\(=x^2-2x+1+2\)
\(=\left(x-1\right)^2+2\ge2\forall x\)
Đẳng thức xảy ra khi \(\left(x-1\right)^2=0\Rightarrow x=1\)
Bài 2:
\(2x^2+4x+11=2x^2+4x+2+9\)
\(=2\left(x^2+2x+1\right)+9\)
\(=2\left(x+1\right)^2+9\ge9>0\forall x\)

\(A=\frac{y}{x}\cdot\sqrt{\frac{x^2}{y^4}}=\frac{y}{x}\cdot\frac{\sqrt{x^2}}{\sqrt{y^4}}=\frac{y}{x}\cdot\frac{\left|x\right|}{\left|y^2\right|}=\frac{y}{x}\cdot\frac{x}{y^2}=\frac{1}{y}\)( x > 0 ; y > 0 )


\(\dfrac{\left(x+16\right)\left(x+9\right)}{x}=\dfrac{x^2+25x+144}{x}=x+25+\dfrac{144}{x}\)
Ta có:
x+\(\dfrac{144}{x}\)\(\ge\)2\(\sqrt{x.\dfrac{144}{x}}\)=2.12=24(dựa vào định lí côsi)
\(\Leftrightarrow\)x+25+\(\dfrac{144}{x}\)\(\ge\)24+25=49
Vậy GTNN của A là 49
\(A=\left(\dfrac{1}{x+2\sqrt{x}}-\dfrac{1}{\sqrt{x}+2}\right):\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\left(x>0;x\ne1\right)\)
\(A=\left[\dfrac{1}{\sqrt{x}\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right]:\dfrac{1-\sqrt{x}}{\left(\sqrt{x}\right)^2+2\cdot\sqrt{x}\cdot2+2^2}\)
\(A=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}:\dfrac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}\)
\(A=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(A=\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
Vậy: ...