Giải pt:
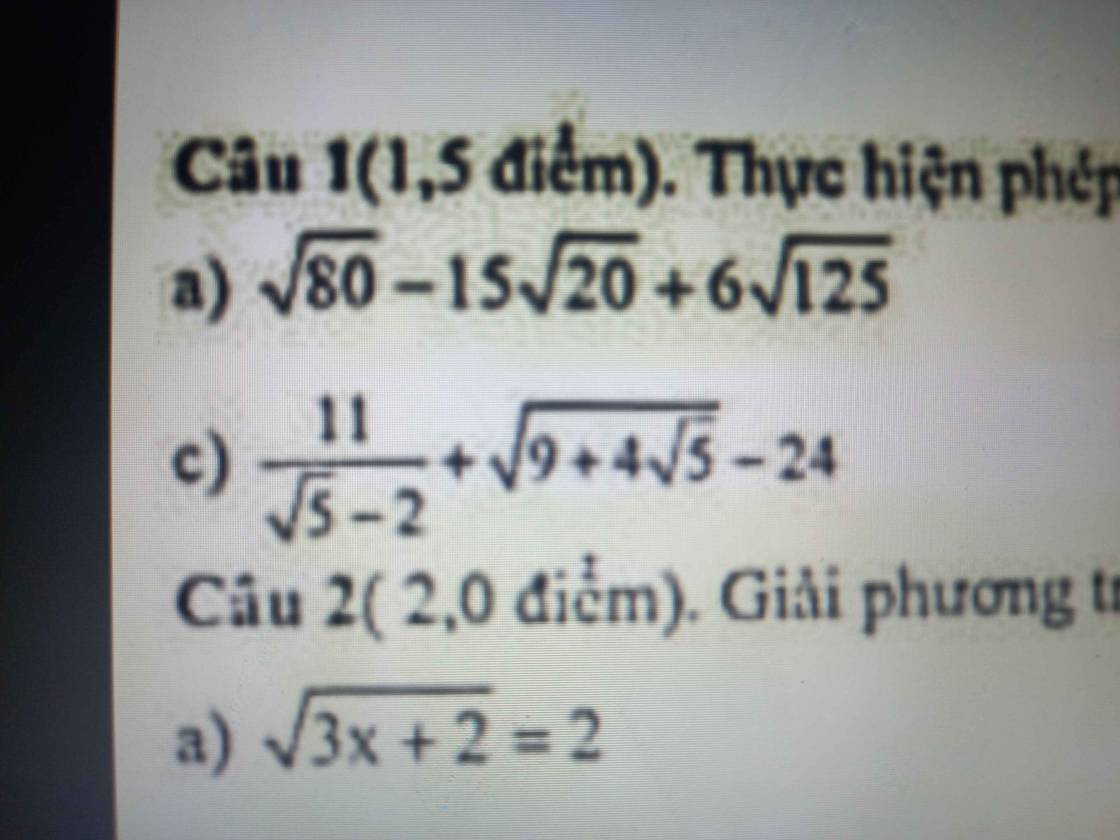 câu 1 ý c ạ
câu 1 ý c ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
3: ĐKXĐ: x>=1
\(x-\sqrt{x+3+4\sqrt{x-1}}=1\)
=>\(x-\sqrt{x-1+2\cdot\sqrt{x-1}\cdot2+4}=1\)
=>\(x-\sqrt{\left(\sqrt{x-1}+2\right)^2}=1\)
=>\(x-\left|\sqrt{x-1}+2\right|=1\)
=>\(x-\left(\sqrt{x-1}+2\right)=1\)
=>\(x-\sqrt{x-1}-2-1=0\)
=>\(x-1-\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}+\sqrt{x-1}-2=0\)
=>\(\left(\sqrt{x-1}-2\right)\left(\sqrt{x-1}+1\right)=0\)
=>\(\sqrt{x-1}-2=0\)
=>\(\sqrt{x-1}=2\)
=>x-1=4
=>x=5(nhận)

\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)

\(x^4+3x^2=0\)
Có \(x^4\ge0;\forall x\); \(3x^2\ge0;\forall x\)
=> VT\(\ge0;\forall x\)
Dấu = xảy ra <=> x=0
Ý C


\(\left(2x-3\right)\left(2x+3\right)=2\left(2x-3\right)\left(2x-3\right)\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3\right)-2\left(2x-3\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(2x+3-4x+6\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(-2x+9\right)=0\)
\(\Leftrightarrow2x-3=0\) hay \(-2x+9=0\)
\(\Leftrightarrow x=\dfrac{3}{2}\) hay \(x=\dfrac{9}{2}\)
-Vậy \(S=\left\{\dfrac{3}{2};\dfrac{9}{2}\right\}\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x^2-1>=0\\2x-1>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\x^2>=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow x>=\dfrac{\sqrt{2}}{2}\)
PT\(\Leftrightarrow\sqrt{2x^2-1}-1+x\sqrt{2x-1}-x=2x^2-x-1\)
\(\Leftrightarrow\dfrac{2x^2-1-1}{\sqrt{2x^2-1}+1}+x\cdot\dfrac{2x-1-1}{\sqrt{2x-1}+1}=\left(x-1\right)\left(2x+1\right)\)
=>\(\dfrac{2\left(x-1\right)\left(x+1\right)}{\sqrt{2x^2-1}}+2x\cdot\dfrac{x-1}{\sqrt{2x-1}+1}-\left(x-1\right)\left(2x+1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{2x+2}{\sqrt{2x^2-1}}+\dfrac{2x}{\sqrt{x-1}+1}-2x-1\right)=0\)
=>x-1=0
=>x=1
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

Vận tốc ca nô so với dòng nước
Th xuôi dòng:\(v_t+v_n=\dfrac{s}{t}\Rightarrow v_t+6=\dfrac{s}{3}\left(1\right)\)
Th ngược dòng:\(v_t-v_n=\dfrac{s}{t'}\Rightarrow v_t-6=\dfrac{s}{4}\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow v_t=42\left(\dfrac{km}{h}\right);s=144\left(km\right)\)
Vậy ...
<Nếu bạn không hiểu chỗ nào thì comment bên dưới nha. Mình sẵn lòng giải đáp câu hỏi đó>

a, Th1 : \(m-1=0\Rightarrow m=1\)
\(\Rightarrow-x+3=0\\ \Rightarrow x=3\)
Th2 : \(m\ne1\)
\(\Delta=\left(-1\right)^2-4.\left(m-1\right).3\\ =1-12m+12\\=13-12m \)
phương trình có nghiệm \(\Delta\ge0\)
\(\Rightarrow13-12m\ge0\\ \Rightarrow m\le\dfrac{13}{12}\)
b, Áp dụng hệ thức vi ét : \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{m-1}\\x_1x_1=\dfrac{3}{m-1}\end{matrix}\right.\)
Tổng bình phương hai nghiệm bằng 12 \(\Rightarrow x^2_1+x^2_2=12\)
\(\left(x_1+x_2\right)^2-2x_1x_2=12\\ \Leftrightarrow\left(\dfrac{1}{m-1}\right)^2-2.\left(\dfrac{3}{m-1}\right)=12\\ \Leftrightarrow\dfrac{1}{\left(m-1\right)^2}-\dfrac{6}{m-1}=12\\ \Leftrightarrow1-6\left(m-1\right)=12\left(m-1\right)^2\\ \Leftrightarrow1-6m+6=12\left(m^2-2m+1\right)\\ \Leftrightarrow7-6m-12m^2+24m-12=0\\ \Leftrightarrow-12m^2+18m-5=0\\ \Leftrightarrow\left[{}\begin{matrix}m=\dfrac{9-\sqrt{21}}{12}\\m=\dfrac{9+\sqrt{21}}{12}\end{matrix}\right.\Rightarrow m=\dfrac{9+\sqrt{21}}{12}\)