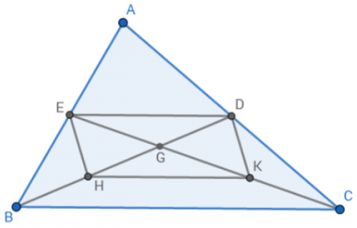
1) Cho tam giác nhọn ABC, các đường cao BD, CE Gọi H và K lần lượt là hình chiếc của B và C lên DE
a) Cmr EH=DK
b) Nếu tam giác ABC cân ở A thì tứ giác BCHK là hình gì??
2) Cho tam giác vuông cân ABC,góc C vuông. M là 1 đ' trên cạnh AB, kẻ \(MR⊥AC,MC⊥BC\)
a) Cmr Cm và RS = nhau và cắt nhau tại trung điểm của mỗi đường
b) GỌi O là tđ' của AB. Tam giác ORS là tam giác gì
Giúp mk nha! Mk đang cần gấp !!!!!!CẢM ƠN nhiều