Cho tam giác ABC nhọn biết AB

JD

Jenny Đặng

25 tháng 10 2023 - olm

Cho tam giác ABC nhọn biết AB<AC . Các đường cao BE , CF cắt nhau tại H . Gọi M là trung điểm của BC . Trên tia đối của tia MH lấy K sao cho MH=MK . a) cm tứ giác BHCK là hbh b) cm BK vuông góc với AB , CK vuông góc với AC c) cm tam giác MEF là tam giác cân d) vẽ CQ vuông góc với BK tại Q . Chứng minh EF vuông góc với...

Đọc tiếp

#Toán lớp 8

0

AT

Anh Thu Ngo

18 tháng 2 2021

cho tam giác nhọn abc .kẻ ah vuông góc bc .Biết AB = 13, AH = 12, HC = 16 .Tính chu vi tam giác ABC

#Toán lớp 7

3

SI

Shiba Inu

18 tháng 2 2021

* Tự vẽ hình nha !

Xét $△ A H B$ vuông tại H, ta có:

BH² = AB² - AH² (Py-ta-go)

BH² = 13² - 12² = 25

=> BH = $\sqrt{25} = 5$ (cm)

Xét $△ A H C$ vuông tại H, ta có:

AC² = AH² + HC² (Py-ta-go)

AC² = 12² + 16² = 400

=> AC = $\sqrt{400} = 20$ (cm)

Ta có: BC = BH + HC = 5 + 16 = 21 (cm)

Chu vi tam giác ABC:

AB + AC + BC = 13 + 20 + 21 = 54 (cm)

Vậy ....................

Đúng(2)

PY

Phong Y

18 tháng 2 2021

https://hoc247.net/hoi-dap/toan-7/tinh-chu-vi-tam-giac-abc-biet-ab-13cm-ah-12cm-va-hc-16cm-faq407733.html

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

21 tháng 9 2023

Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

#Toán lớp 7

1

KS

Kiều Sơn Tùng

21 tháng 9 2023

Tham khảo:

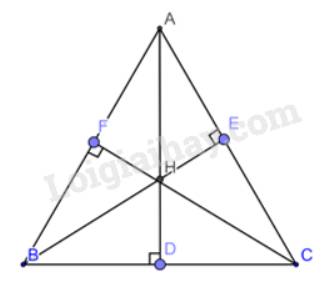
Xét tam giác BFC và tam giác BEC có :

BC chung

FC = BE

$\widehat {BFC} = \widehat {BEC} = {90^o}$

( cạnh huyền – cạnh góc vuông)

$ \Rightarrow \widehat C = \widehat B$ ( 2 góc tương ứng ) (1)

Xét tam giác CFA và tam giác ADC ta có :

CF = AD

AC chung

$\widehat {ADC} = \widehat {AFC} = {90^o}$

(cạnh huyền – cạnh góc vuông)

$ \Rightarrow \widehat C = \widehat A$(2 góc tương ứng ) (2)

Từ (1) và (2) $ \Rightarrow \widehat C = \widehat A = \widehat B$ $ \Rightarrow $Tam giác ABC là tam giác đều do có 3 góc bằng nhau

Đúng(0)

PH

Phạm Hà Chi

6 tháng 1 2018 - olm

1.Cho tam giác ABC nhọn, vẽ đường cao AH. Tính chu vu của tam giác ABC, biết AC = 13cm, AH = 12 cm, BH = 9cm

2. Cho tam giác ABC, góc A = 90 độ. BIết AB + AC = 49 cm; AB - AC = 7cm. Tínnh BC

3. Cho tam giác ABC, AB = AC =17 cm. Kẻ BD vuông góc với AC. Tính BC biết BD = 15cm

#Toán lớp 7

0

NL

Nguyễn Lam Giang

20 tháng 2 2020 - olm

Cho tam giác ABC nhọn. Kẻ AH ^BC (HÎBC). Tính chu vi của tam giác ABC biết AB = 10cm, AH = 8cm, HC = 5cm.

#Toán lớp 7

8

NL

Nguyễn Lam Giang

20 tháng 2 2020

AH vuông góc vs BC ( H thuocj BC ) nha

Đúng(0)

A

̿๖ۣۜɦ๏àйǥ๖ۣۜϮử๖ۣۜáйɦ๖ۣۜϮɾăйǥッ

20 tháng 2 2020

kẻ ah vuông góc vs bc ak

Đúng(0)

NH

nguyễn huy tuấn

18 tháng 2 2020 - olm

Cho tam giác ABC nhọn. kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4cm, HC = 12cm

#Toán lớp 7

1

NN

Nguyễn Nam Dương

24 tháng 12 2021

Áp dụng định lý Pitago, ta có: $AC^2=AH^2+HC^2$

$\Rightarrow20^2=12^2+HC^2$

$\Rightarrow HC^2=20^2-12^2$

$\Rightarrow HC^2=400-144=256$

$\Rightarrow HC=16\left(cm\right)$

Áp dụng định lý Pitago, ta có: $AB^2=BH^2+AH^2$

$\Rightarrow AB^2=5^2+12^2$

$\Rightarrow AB^2=25+144=169$

$\Rightarrow AB=13\left(cm\right)$

Vậy CV tam giác ABC là

$20+5+16+13=54\left(cm\right)$

Đúng(0)

DV

Dương Văn Tiến

7 tháng 5 2022 - olm

a) tính số đo mỗi góc nhọn của tam giác ABC vuông cân tại A

b) cho tam giác ABC . Biết AB=11cm;AC=15cm; BC=19cm

so sánh các góc của tam giác ABC

#Toán lớp 7

1

CT

CTD Thành

7 tháng 5 2022

a, Do ABC vuông cân
=> Góc A = 90 độ
=> Góc B = Góc C = 90/2 = 45 độ
b, Do AB < AC < BC (11 < 15 < 19)
=> Góc C < Góc B < Góc A (Quan hệ góc đối diện)

Đúng(1)

PT

Phạm thị thảo

7 tháng 2 2018 - olm

Cho tam giác ABC nhọn . Kẻ AH vuông góc với BC. Tính chu vi của tam giác ABC . Biết AB = 5cm, AH=4cm, HC=12cm

#Toán lớp 7

1

OS

Otoshiro Seira

3 tháng 3 2018

Ta có:$AC^2=HC^2+AH^2$(Định lý pytago)

$\Rightarrow AH^2=AC^2-HC^2=4^2-2^2=16-4=12$

$\Rightarrow AH=\sqrt{12}\approx3$

Độ dài BC là :3+2=5

Chu vi của tam giác ABC la:$4+5+5\approx14$

Đúng(0)

PN

Phạm Ngọc Mai

13 tháng 3 2021 - olm

Cho tam giác nhọn ABC. Kẻ AH ⊥ BC (H∈BC). Biết AB = 13 cm; AH = 12 cm và HC=16 cm. Tính chu vi tam giác ABC.

#Toán lớp 7

6

PN

Phạm Ngọc Mai

13 tháng 3 2021

Mọi người giúp em nhanh với🥺👉👈

Đúng(0)

VV

Vi Văn Tuấn

13 tháng 3 2021

CÁC BN THỬ VÀO TRANG CÁ NHÂN CỦA MIK ĐI, BẤT NGỜ LẮM

Đúng(0)

DD

Dracula Darklork

26 tháng 7 2016 - olm

cho tam giác nhọn ABC KẺ AH vuông góc BC.Tính chu vi tam giác biết AB=5cm,AH=4cm,HC=12cm

#Toán lớp 7

0

TH

Trịnh Hà 7e

24 tháng 11 2016 - olm

CHO tam giác nhọn ABC tính p của tam giác ABC biết AB bằng 5cm, AH bằng 4cm ,HC bằng 12CM kẻ AH vuông góc với BC

#Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP