giúp mình với
Cho biết x + y = 5. Tìm GTLN của P = x y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

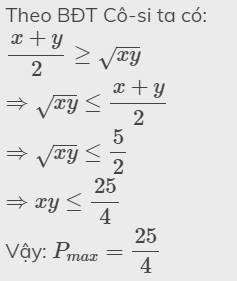

Có:
\(\frac{x}{\sqrt{y}}+\sqrt{y}\ge2\sqrt{x};\frac{y}{\sqrt{x}}+\sqrt{x}\ge2\sqrt{y}\)
Cộng theo vế suy ra: \(\frac{x}{\sqrt{y}}+\frac{y}{\sqrt{x}}+\sqrt{x}+\sqrt{y}\ge2\sqrt{x}+2\sqrt{y}\)
\(\Rightarrow\frac{x}{\sqrt{y}}+\frac{y}{\sqrt{x}}-\sqrt{x}-\sqrt{y}\ge0\)
Đẳng thức xảy ra khi x = y

Áp dụng bổ đề \(\left|a\right|-\left|b\right|\le\left|a-b\right|\)
Ta có \(A=\left|x-\sqrt{2}\right|+\left|y-1\right|\ge\left|x\right|+\left|y\right|-\left(\left|\sqrt{2}\right|+1\right)\)
\(\Rightarrow A\ge5-\sqrt{2}-1=4-\sqrt{2}\)
Mình mới biết làm Min thôi , thông cảm :>>

1.
\(P=x^2+6y+10+y^2-x\)
\(=x^2-2\times x\times\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+y^2+2\times y\times3+3^2-3^2+10\)
\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\)
\(\left(x-\frac{1}{2}\right)^2\ge0\)
\(\left(y+3\right)^2\ge0\)
\(\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy Min P = \(\frac{3}{4}\) khi x = \(\frac{1}{2}\) và y = \(-3\)
2.
\(N=x-x^2\)
\(=-\left(x^2-2\times x\times\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\right)\)
\(=-\left[\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\right]\)
\(\left(x-\frac{1}{2}\right)^2\ge0\)
\(\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\ge-\frac{1}{4}\)
\(-\left[\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\right]\le\frac{1}{4}\)
Vậy Max N = \(\frac{1}{4}\) khi x = \(\frac{1}{2}\)