Cho tam giác ABC .CMR:
a.Nếu đường thẳng m song song với cạnh BC thì m sẽ cắt các đường thẳng AB,AC.
b.Nếu đường thẳng m song song với cạnh BC và cắt cạnh AB thì m sẽ cắt cạnh AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì m song song với BC
và AB cắt BC tại B
nên m cắt AB
Vì m//BC
và AC cắt BC tại C
nên m cắt AC
b: Vì m//BC
và BC cắt AC
nên m cắt AC

a: m//BC
BC cắt AB tại B
Do đó: m cắt AB
m//BC
BC cắt AC tại C
Do đó: m cắt AC
b: m//BC
BC cắt AC
Do đó: m cắt AC

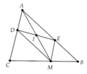
Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)

Hình bạn tự vẽ!
a) Giả sử m không cắt \(AB,AC\). Thật vậy
=> \(m\) // \(AB\) và \(m\) // \(BC.\)
=> \(AB\) // \(AC\) // \(BC\) (vô lí với gt \(\Delta ABC\))
=> \(m\) sẽ cắt các đường thẳng \(AB,AC.\)
Vậy ta có đpcm.
b) Gỉa sử m không cắt \(AC.\) Thậy vậy
=> \(m\) // \(AC\)
=> \(AC\) // \(BC\) (vô lí với gt \(\Delta ABC\))
=> \(m\) sẽ cắt cạnh \(AC.\)
Vậy ta có đpcm.
Chúc bạn học tốt!
a) Giả sử m không cắt AB, AC. Thật vậy ta suy ra m // AB và m // AC. Suy ra AB // AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
b) Giả sử m không cắt AC. Thật vậy ta suy ra m // AC. Suy ra AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
bn vẽ hình cho mình đc k