Đơn giản các biểu thức sau ( giả sử các biểu thức sau đều có nghĩa )
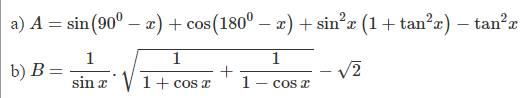
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(sin^4x+cos^4x=\left(sin^2x\right)^2+\left(cos^2x\right)^2\)
\(=\left(sin^2x\right)^2+2sin^2xcos^2x+\left(cos^2x\right)^2-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\)
b) \(\dfrac{1+cotx}{1-cotx}=\dfrac{tanx.cotx+cotx}{tanx.cotx-cotx}\)
\(=\dfrac{cotx.\left(tanx+1\right)}{cotx.\left(tanx-1\right)}\)
\(=\dfrac{tanx+1}{tanx-1}\)
c) \(\dfrac{cosx+sinx}{cos^3x}=\dfrac{1}{cos^2x}+\dfrac{tanx}{cos^2x}\)
\(=1+tan^2x+tanx.\dfrac{1}{cos^2x}\)
\(=1+tan^2x+tanx.\left(1+tan^2x\right)\)
\(=1+tan^2x+tanx+tan^3x\)
\(=tan^3x+tan^2x+tanx+1\)

Lời giải:
a.
$\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-2\sin ^2x\cos ^2x$
b.
$\frac{1+\cot x}{1-\cot x}=\frac{1+\frac{\cos x}{\sin x}}{1-\frac{\cos x}{\sin x}}=\frac{\cos x+\sin x}{\sin x-\cos x}(1)$
$\frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}+1}{\frac{\sin x}{\cos x}-1}=\frac{\cos x+\sin x}{\sin x-\cos x}(2)$
Từ $(1); (2)$ ta có đpcm
c.
$\frac{\cos x+\sin x}{\cos ^3x}=(1+\frac{\sin x}{\cos x}).\frac{1}{\cos ^2x}$
$=(1+\tan x).\frac{\sin ^2x+\cos ^2x}{\cos ^2x}$
$=(1+\tan x)(\tan ^2x+1)=\tan ^3x+\tan ^2x+\tan x+1$
Ta có đpcm.

1234567890-01234567890-=qưertyuiop[]\';;lkjhfgdsazxcvbnm,./\'l;[]7894561230.+-
a) \(A=sin\left(90^0-x\right)+cos\left(180^0-x\right)+sin^2x\left(1+tan^2x\right)-tan^2x\)
\(=cosx-cosx+sin^2x.\left(\dfrac{1}{cos^2x}\right)-tan^2x\)
\(=tan^2x-tan^2x\)
\(=0\)
b) \(B=\dfrac{1}{sinx}.\sqrt{\dfrac{1}{1+cosx}+\dfrac{1}{1-cosx}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{1-cosx+1+cosx}{1-cos^2x}}-\sqrt{2}\)
\(=\dfrac{1}{sinx}.\sqrt{\dfrac{2}{sin^2x}}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}}{sin^2x}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}\left(1-sin^2x\right)}{sin^2x}\)
\(=\dfrac{\sqrt{2}cos^2x}{sin^2x}\)
\(=\sqrt{2}tan^2x\)