mong mn giúp nốt bài này ạ

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



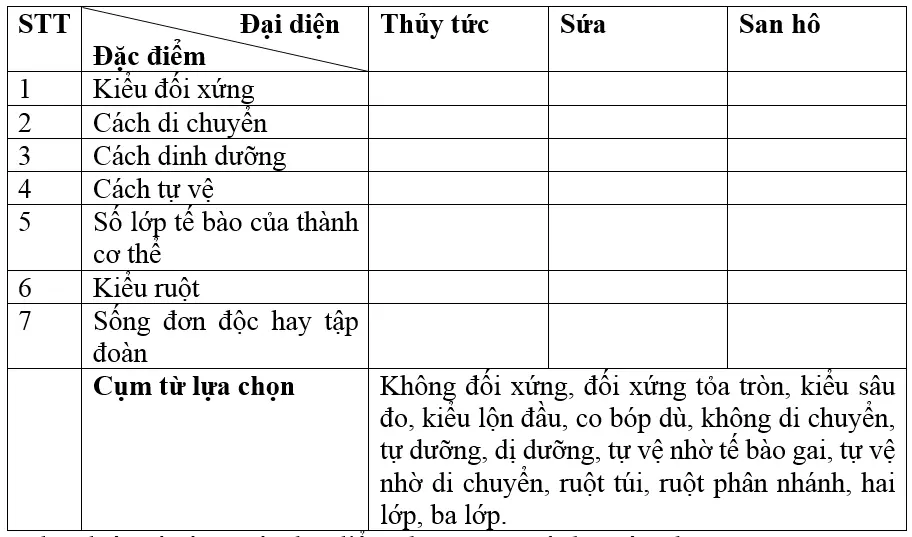
-Đặc điểm chung của ngành ruột khoang là:
+ Cơ thể đối xứng tỏa tròn.
+ Sống dị dưỡng.
+ Thành cơ thể gồm 2 lớp tế bào, giữa là tầng keo.
+ Ruột dạng túi.
+ Tấn công và tự vệ bằng tế bào gai.
-
* Lợi ích
- Trong tự nhiên:
+ Có ý nghĩa sinh thái đối với biển và đại dương: cung cấp thức ăn và nơi ẩn nấp cho một số động vật.
+ Tạo cảnh quan thiên nhiên độc đáo, là điều kiện để phát triển du lịch: đảo san hô vùng nhiệt đới.
- Đối với đời sống:
+ Là nguyên liệu làm đồ trang sức, trang trí: vòng tay làm bằng san hô.
+ Làm vật liệu xây dựng: san hô đá.
+ Là vật chỉ thị cho tầng địa chất: hóa thạch san hô.
+ Làm thực phẩm: gỏi sứa.
* Tác hại
- Một số loài sứa gây ngứa và độc: sứa lửa.
- Cản trở giao thông đường biển: đảo san hô ngầm.
-Trâu, bò.
-
- Cấu tạo:
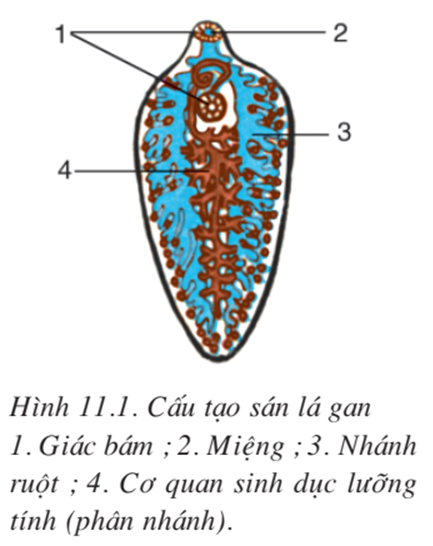
+ Cơ thể hình lá, dẹp, dài 2 – 5cm, đối xứng 2 bên màu đỏ máu.
+ Mắt, lông bơi tiêu giảm giúp thích nghi với đời sống kí sinh không di chuyển.
+ Các giác bám phát triển để bám vào vật chủ.
tác hại và lợi ích của ngành ruột khoang

môi trường sống của sán lá gan
– Sán lông thường sống ở vùng nước ven biển, ao, hồ,…
-Bơi nhẹ nhàng trong nước hoặc trượt trên giá thể
+vật chủ chính là động vật ăn cỏ như trâu, bò, cừu; người chỉ là vật chủ ngẫu nhiên, tình cờ mắc bệnh; vật chủ trung gian truyền bệnh là ốc họ Lymnaea.
– Hình lá, có đầu bằng, 2 bên có thùy khứu giác, mắt và lông bơi phát triển. Dẹp theo hướng lưng bụng, miệng nằm ở mặt bụng, tiếp theo miệng là các nhánh ruột, chưa có hậu môn, đuôi hơi nhọn.


what is her mother going to prepare for her bỉthdat party
a: Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)
b:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=6^2-3^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{6}\)
=>\(\dfrac{AD}{1}=\dfrac{CD}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{1}=\dfrac{CD}{2}=\dfrac{AD+CD}{1+2}=\dfrac{3\sqrt{3}}{3}=\sqrt{3}\)
=>\(\left\{{}\begin{matrix}AD=\sqrt{3}\simeq1,7\left(cm\right)\\CD=2\sqrt{3}\simeq3,5\left(cm\right)\end{matrix}\right.\)
c: ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot6=3\cdot3\sqrt{3}=9\sqrt{3}\)
=>\(AH=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
d: ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\left(1\right)\)
ΔADB vuông tại A có AE là đường cao
nên \(BE\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BE\cdot BD\)
=>\(\dfrac{BH}{BD}=\dfrac{BE}{BC}\)
Xét ΔBHE và ΔBDC có
BH/BD=BE/BC
\(\widehat{HBE}\) chung
Do đó: ΔBHE đồng dạng với ΔBDC