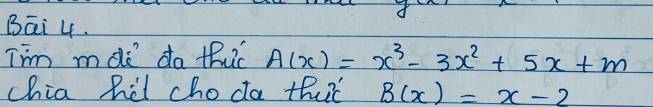 sossssssssssss gấp
sossssssssssss gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tập con của tập A gồm n phần tử là 2^n
Thật vậy, bằng quy nạp ta có :
Với n=0, tập rỗng có 2^0=1 tập con. Đúng.
Với n=1, có 2^1 = 2 tập con là rỗng và chính nó. Đúng.
Giả sử công thức đúng với n=k. Tức là số tập con của tập hợp gồm k phần tử là 2^k
Ta phải chứng minh công thức đúng với k+1.
Ngoài 2^k tập con vốn có, thêm cho mỗi tập cũ phần tử thứ k + 1 thì được một tập con mới. Vậy ta được 2^k tập con mới. Tổng số tập con của tập hợp gồm k + 1 phần tử (tức tổng số tập con của tập gồm 2^k phần tử và tập con mới tạo thành) là : 2^k + 2^k = 2^k . 2 = 2 ^(k+1). Đúng
Vậy số tập con của tập A gồm n phần tử là 2^n
đúng ko bn
nếu **** thì tk mk nha
:3


A=1/5x6+1/6x7+..+1/17x18
=1/5-1/6+1/6+1/7+...+1/17-1/18
=1/5-1/18=13/90.

nếu muốn 59xy chia hết cho 9 thì:
5+9=14
tông này ko chia hết cho 9 nên ta phai cộng thêm 1 số ko chia hết cho 9
mà x-y =3
vậy x là 5
y là 2
=5952
kiểm tra:5+2=7,14+7=21 chia hết cho 9
5-2=3



Do A(x) chia hết cho \(B\left(x\right)=x-2\)
Nên A(x) sẽ nhận \(x=2\) là nghiệm thay vào ta có:
\(2^3-3\cdot2^2+5\cdot2+m=0\)
\(\Leftrightarrow8-3\cdot4+10+m=0\)
\(\Leftrightarrow18-12+m=0\)
\(\Leftrightarrow6+m=0\)
\(\Leftrightarrow m=-6\)
Vậy khi m=-6 thì A(x) chia hết cho B(x)