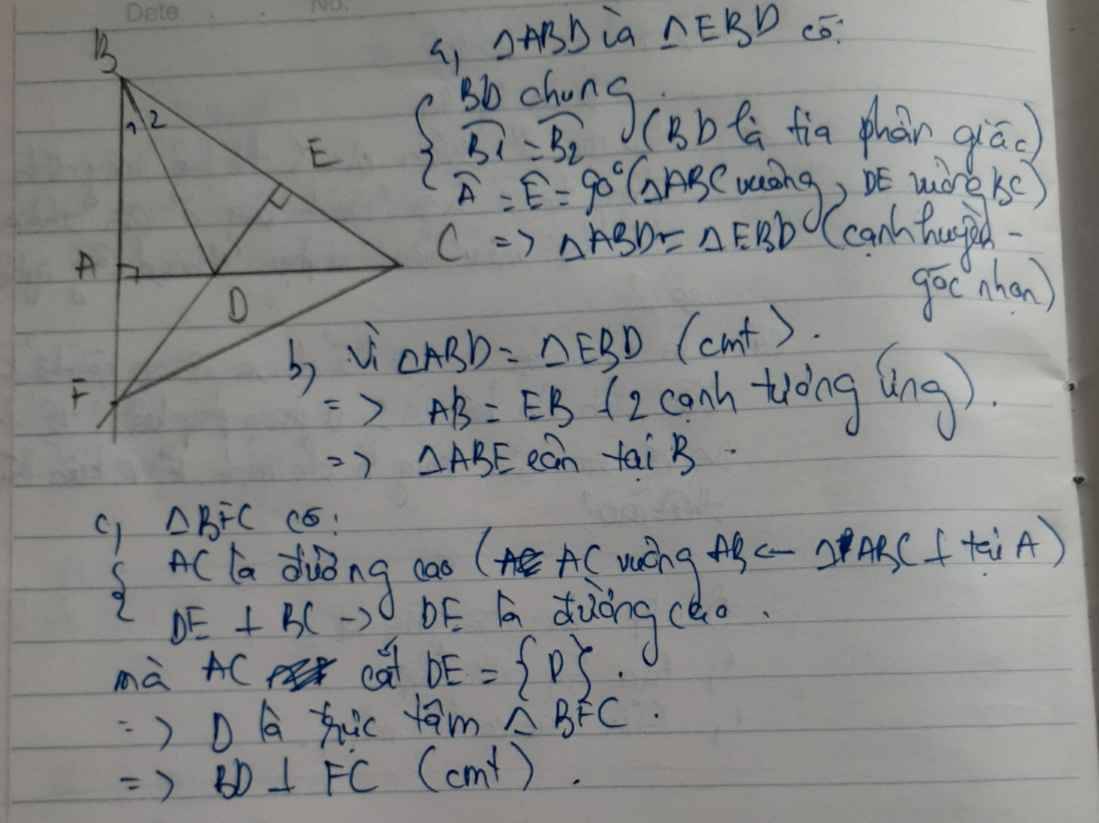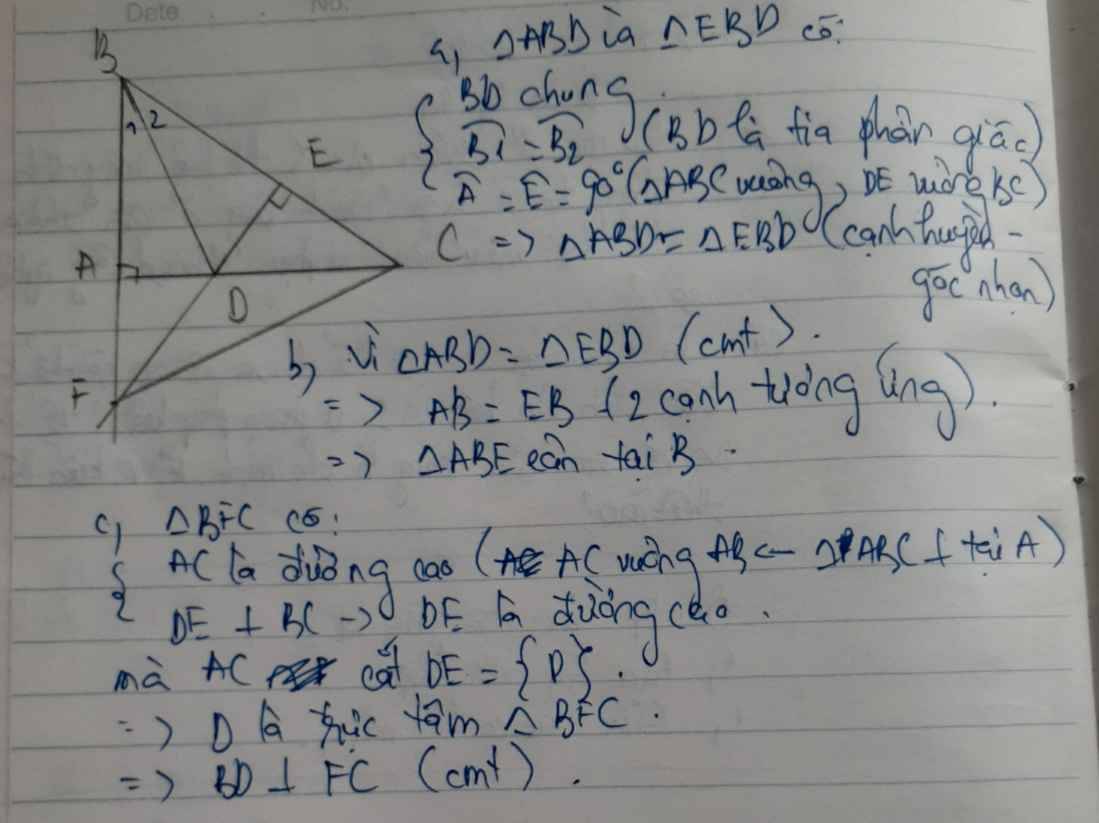Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC . Tia phân giác của HAC cắt BC tại K. Hỏi tam giác AKB là tam giác gì? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2021
a) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)
b) Ta có: \(\widehat{BDA}+\widehat{DAH}=90^0\)
\(\widehat{BAD}+\widehat{KAD}=90^0\)
mà \(\widehat{DAH}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
nên \(\widehat{BDA}=\widehat{BAD}\)
Xét ΔABD có \(\widehat{BDA}=\widehat{BAD}\)(cmt)
nên ΔABD cân tại B(Định lí đảo của tam giác cân)
c) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
9 tháng 8 2015
a) Áp dụng định lí Pi-Ta-go vào ΔABC :
\(AC^2=BC^2-AB^2=10^2-6^2=64\)
\(AC=\sqrt{64}=8\left(cm\right)\).
b) ΔABK có BE vừa là đường cao vừa là trung tuyến nên tam giác ABk là tam giác cân.( nếu bạn chưa học tính chất này thì xét 2 tam giác BEA và BEK cũng được, điều kiện xét đã có sẵn r).
c) Xét ΔABD và ΔKBD có:
AB=AK(ΔABK cân tại B)
Góc ABD=KBD(gt)
BD cạnh chung
Vậy ΔABD=ΔKBD(c.g.c)
=> Góc BAD=BKD=90o(hai góc tương ứng)
hay DK vuông góc với BC
d) Vì DK vuông góc với BC
AH vuông góc với BC
nên DK//AH => Góc DKA=HAK(so le trong) (1)
Vì ΔABD=KBD(cmt) => AD=KD(2 cạnh tương ứng) hay tam giác ADK cân tại K
=> Góc DKA=DAK hay DKA=CAK (2)
Từ (1) và (2) suy ra Góc HAK=CAK
Hay AK là tia phân giác của góc HAC.
DT
17 tháng 4 2019
bn tham khảo câu hỏi của bn Viêt Thanh Nguyễn Hoàng nhé, bài ấy mik cx làm đấy
PN
1 tháng 5 2020
a) Có tam giác ABC vuông tại A
=>BC2=AC2+AB2 ( định lí Pitago)
=>BC2=82+62=100
=> BC=10 (cm)
b) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
Góc DBA= góc DBK hay góc EBA= góc EBK ( vì BD là tia phân giác của góc ABC)
=> tam giác ABE= tam giác KBE( cạnh góc vuông- góc nhọn)
=> BA=BK ( 2 cạnh tương ứng)
Vạy tam giác ABK cân tại B
c) Nối D với K, ta có tam giác DKE vuông tại E
Theo câu b, ta có tam giác ABE= tam giác KBE
=> KE=EA( 2 cạnh tương ứng) và góc EAB=góc EKB (1)
Xét tam giác vuông DEA và tam giác vuông DEK có
Cạnh DE chung
EA=KE
=> tam giác DEA= tam giác DEK ( 2 cạnh góc vuông)
=> Góc DAE=góc DKE (2)
Từ (1) và (2) =>góc DKE+ góc EKB=góc DAE+ góc EAB= góc DAB=90 độ
=> Góc DKB= 90 độ
Vậy DK vuông góc với BC
CU
17 tháng 2 2019
chị tự kẻ hình :
AH _|_ BC (gt) => góc DHA = 90o (đn)
=> góc ADH + góc DHA + góc DAH = 180 (đl)
=> góc ADH + 90 + góc DAH = 180
=> góc ADH = 180 - 90 - góc DAH
=> góc ADH = 90 - góc DAH (1)
có tam giác ABC vuông tại A (gt)
=> góc DAB + góc CAD = 90
=> góc DAB = 90 - góc CAD (2)
AD là phân giác của góc HAC (gt) => góc CAD = góc DAH (đn) (3)
(1)(2)(3) => góc DAB = góc ADB
=> tam giác ABD cân tại B (dh)
