giải cho em với ạ em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 8 2021
a: Xét tứ giác MNKP có
MN//KP
MP//NK
Do đó: MNKP là hình bình hành
Suy ra: MP=NK
mà MP=NQ
nên NK=NQ
Xét ΔNQK có NK=NQ
nên ΔNQK cân tại N
b: Xét ΔMQP và ΔNPQ có
MQ=NP
MP=NQ
QP chung
Do đó: ΔMQP=ΔNPQ
D
25 tháng 1 2022
23.
- Gọi E là trung điểm AB.
- Xét tam giác ABH vuông tại H có:
\(\widehat{ABH}+\widehat{BAH}=90^0\) (kề phụ)
=>\(\widehat{ABH}+30^0=90^0\)
=>\(\widehat{ABH}=90^0-30^0=60^0\).
- Xét tam giác ABH vuông tại H có:
HE là trung tuyến ứng với cạnh huyền AB (E là trung điểm AB).
=>\(HE=BE=\dfrac{1}{2}AB\).
=>Tam giác BEH cân tại E.
Mà \(\widehat{EBH}=60^0\)(cmt)
=>Tam giác BEH đều.
=>\(BH=HE=BE=\dfrac{1}{2}AB\)
=>AB=2.BH=2.3,1=6,2 (cm).
* SABCD=6,2.3,1=19,22 (cm2).
24.- Ta có: SABCD=\(\dfrac{1}{2}AC.BD\)=48m2
=>AC.BD=24m2.
- Ta có: \(\dfrac{AC}{BD}=\dfrac{2}{3}\)(gt) =>AC=\(\dfrac{2}{3}BD\)
=>\(\dfrac{2}{3}BD^2\)=24 =>BD=6cm.
=>AC=\(\dfrac{2}{3}.6=4\)(cm)
25 tháng 1 2022
a: \(S=\dfrac{10\cdot24}{2}=24\cdot5=120\left(cm^2\right)\)
b: Cạnh của hình thoi là:
\(\sqrt{5^2+12^2}=13\left(cm\right)\)
Chu vi là 13x4=52(cm)
21 tháng 3 2022
\(n_{Fe}=\dfrac{11,2}{56}=0,2\left(mol\right)\\ n_S=\dfrac{3,2}{32}=0,1\left(mol\right)\\ PTHH:Fe+S\underrightarrow{t^o}FeS\left(1\right)\\ LTL:0,2>0,1\Leftrightarrow Fe.dư\)
\(Theo.pt\left(1\right):n_{Fe\left(pư\right)}=n_{FeS}=0,1\left(mol\right)\\ n_{FeS\left(dư\right)}=0,2-0,1=0,1\left(mol\right)\)
\(PTHH:FeS+H_2SO_4\rightarrow FeSO_4+H_2S\uparrow\left(2\right)\\ Fe+2H_2SO_4\rightarrow FeSO_4+SO_2\uparrow+2H_2O\left(3\right)\)
\(Theo.pt\left(2\right):n_{H_2S}=n_{FeS}=0,1\left(mol\right)\\ Theo.pt\left(3\right):n_{SO_2}=n_{Fe}=0,1\left(mol\right)\\ \%V_{H_2S}=\dfrac{0,1}{0,1+0,1}=50\%\\ \%V_{SO_2}=100\%-50\%=50\%\)
\(Theo.pt\left(2\right):n_{H_2SO_4\left(2\right)}=n_{FeS}=0,1\left(mol\right)\\ Theo.pt\left(3\right):n_{H_2SO_4\left(3\right)}=2n_{Fe}=2.0,1=0,3\left(mol\right)\\ C_{MddH_2SO_4}=\dfrac{0,3}{0,2}=1,5M\)
DN
1
QN
6 tháng 4 2022
a) Xét ∆ ABM(<A=90°(gt)) và ∆NDM(<N=90°(gt)), ta có:
<BMA=<DMN( đối đỉnh)
BM=DM(gt)
⟹∆ABM=∆NDM(c.h=g.n)
b) Ta có:
<ABM=<MDN(Vì ∆ABM=∆NDM(CM ở a))
mà <ABM=<CBM(gt)
⟹<MDN=<CBM
⟹∆EBD cân tại E
⟹ BE=DE
c)Áp dụng định lý Py-ta-go vào ∆ABC(<A=90°(gt)), ta có:
BC2=AB2+AC2
⟹AB2=BC2-AC2=152-122=225-144=81
⟹AB=√81=9cm
mà AB=DN(Vì ∆ABM=∆NDM(CM ở a))
⟹AB=DN=9cm
NT
3
AH
Akai Haruma
Giáo viên
4 tháng 11 2023
Lời giải:
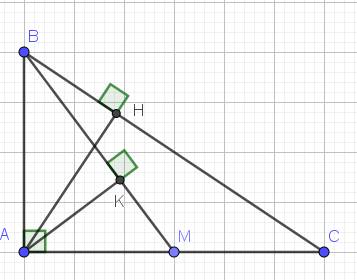
a. Áp dụng hệ thức lượng trong tam giác vuông ta có:
$AH^2=BH.CH=4.6=24$
$\Rightarrow AH=\sqrt{24}=2\sqrt{6}$ (cm)
$AB^2=BH.BC=BH(BH+CH)=4(4+6)=40$
$\Rightarrow AB=\sqrt{40}=2\sqrt{10}$ (cm)
b.
$AC^2=CH.BC=6(6+4)=60$
$\Rightarrow AC=\sqrt{60}=2\sqrt{15}$ (cm)
$AM=AC:2=\sqrt{15}$ (cm)
$\tan \widehat{AMB}=\frac{AB}{AM}=\frac{2\sqrt{10}}{\sqrt{15}}=\frac{2\sqrt{6}}{3}$
$\Rightarrow \widehat{AMB}=59^0$
c.
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $ABM$:
$BK.BM=AB^2(1)$
Áp dụng hệ thức lượng với tam giác $ABC$:
$AB^2=BH.BC(2)$
Từ $(1); (2)\Rightarrow BK.BM=BH.BC$
