4. Cho tam giác ABC có AB = AC, kẻ tia phân giác góc A cắt BC tại E. CMR:
ΔAEB = ΔAEC từ đó suy ra \(AE\perp BC\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2020
a, có AE là pg của ^BAC (gt) ; ^BAC = 60 (gt) => ^DAB = 30
xét tam giác ABC vuông tại C (gt) có ^BAC = 60 (gt) => ^CBA = 30
=> ^DAB = ^CBA
xét tam giác BDA và tam giác ACB có : AB chung
^BDA = ^ACB = 90
=> tam giác BDA = tam giác ACB (ch-gn)
=> AD = BC (Đn)
b, có : ^CBA = ^DAB = 30 (câu a)
=> tam giác BEA cân tại E (dh)
có EK là đường cao (gt)
=> EK đồng thời là đường trung tuyến của tam giác BEA (đl)
=> K là trung điểm của AB (đn)
=> BK = AK (đn)
c, kẻ BD cắt CA tại M
xét tam giác BMA có : AE _|_ BD ; BE _|_ CA; EK _|_ AB
=> AC;EK;BD đồng quy
4 tháng 3 2020
Tự vẽ hình nha
a) ABD và EBD có: abd = ebd (bd la phân giác), BD chung
=> bằng nhau (cạnh huyền - góc nhọn)
=> AB = Be (2 cạnh tương ứng) => abe cân
b) ta có: AD = DE (vì tg ABD = tg EBD) mà DE < CD (Cạnh huyên là cạnh lớn nhất) nên AD < CD (ĐPCM)
27 tháng 6 2015
a) Xét 2 tam giác vuông: ACD và AKD, có:
góc CAD = góc KAD (phân giác AE, gt)
AE là cạnh chung
=> tam giác ACD = tam giác AKD (cạnh huyền - góc nhọn)
=> AK = AC (2 cạnh tương ứng) (đpcm)
b) đề có nhầm ko bạn
10 tháng 4 2023
\(\text{#TNam}\)
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
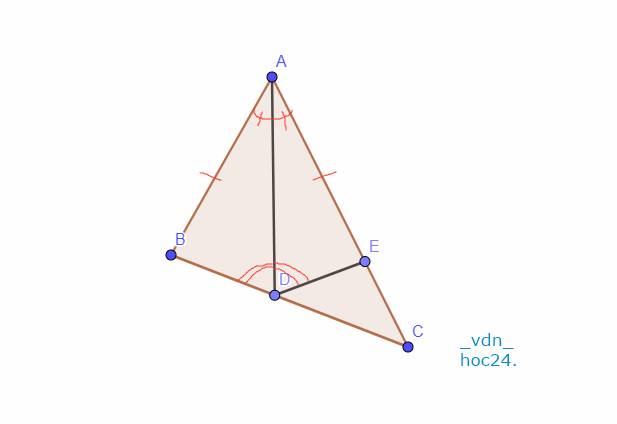
Để chứng minh ΔAEB = ΔAEC, ta có thể sử dụng nguyên lý cắt giao. Vì AB = AC và AE là tia phân giác góc A, nên ta có AE là đường trung trực của đoạn thẳng BC. Từ đó, ta có AE ⊥ BC. Vì AE là đường trung trực của đoạn thẳng BC, nên ta cũng có BE = EC. Như vậy, ta đã chứng minh được ΔAEB = ΔAEC.