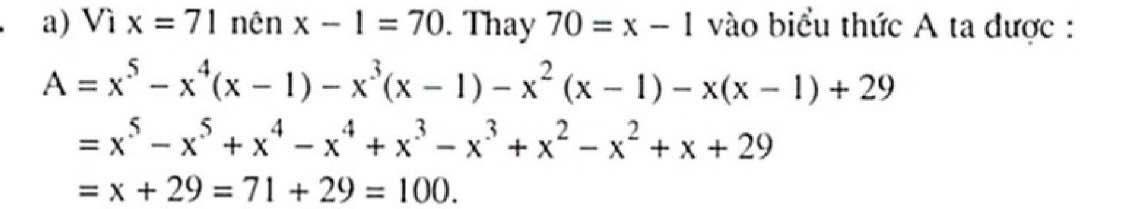A=x^5-70x^4-70x^3-70x^2-70x-+29 tai x=71
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 7 2021
Ta có: x=71
nên x-1=70
Ta có: \(A=x^5-70x^4-70x^3-70x^2-70x^2-70x+29\)
\(=x^5-x^4\left(x-1\right)-x^3\left(x-1\right)-x^2\left(x-1\right)-x\left(x-1\right)+29\)
\(=x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+29\)
=x+29
=71+29
=100
27 tháng 8 2019
Cách 1: Ta có x=71=>x-71=0
A=x5-71x4+x4-71x3+x3-71x2+x2-71x+x-71+100
=x4(x-71)+x3(x-71)+x2(x-71)+x(x-71)+(x-71)+100
=100
Vậy A=100 tại giá trị x=71
Cách 2: vì x=71=>x-1=70
A=x5-(x-1)x4-(x-1)x3-(x-1)x2-(x-1)x+29
=x5-x5+x4-x4+x3-x3+x2-x2+x+29
=x+29=71+29=100
Vậy A=100 tại giá trị x=71
Cách 3: Thay trực tiếp x=71 vào biểu thức A, cách này không hay cho lắm
27 tháng 8 2019
Ta có x=71=>x-71=0
A=x5-71x4+x4-71x3+x3-71x2+x2-71x+x-71+100
=x4(x-71)+x3(x-71)+x2(x-71)+x(x-71)+(x-71)+100
=100
Vậy A=100 tại giá trị x=71
.,.............học tốt................
PD
1
B
23 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
DL
2
LM
8 tháng 7 2018
\(A=x^5-70x^4-70x^3-70x^2-70x+29\) (ở đây mình có sửa đề nha, vì nếu để +70x2 thì sẽ không đúng với quy luật của bài toán và kết quả sẽ rất lớn)\(\Leftrightarrow A=x^5-71x^4+x^4-71x^3+x^3-71x^2+x^2-71x+x-71+100\)\(\Leftrightarrow A=x^4\left(x-71\right)+x^3\left(x-71\right)+x^2\left(x-71\right)+x\left(x-71\right)+\left(x-71\right)+100\)\(\Leftrightarrow A=\left(x-71\right)\left(x^4+x^3+x^2+x+1\right)+100\)
Với x = 71 thì:
\(A=\left(71-71\right)\left(71^4+71^3+71^2+71+1\right)+100\) \(\Leftrightarrow A=0\times\left(71^4+71^3+71^2+71+1\right)+100\)
\(\Leftrightarrow A=100\)
LM
8 tháng 7 2018
Nếu không sửa đề thì bài toán sẽ là:
\(A=x^5-70x^4-70x^3+70x^2-70x+29\)\(\Leftrightarrow A=x^5-71x^4+x^4-71x^3+x^3-71x^2+141x^2-10011x+9941x-705811+705840\)\(\Leftrightarrow A=x^4\left(x-71\right)+x^3\left(x-71\right)+x^2\left(x-71\right)+141x\left(x-71\right)+9941\left(x-71\right)+705840\)\(\Leftrightarrow A=\left(x-71\right)\left(x^4+x^3+x^2+141x+9941\right)+705840\)
Với x = 71 thì:
\(A=\left(71-71\right)\left(71^4+71^3+71^2+141\times71+9941\right)+705840\) \(\Leftrightarrow A=0\times\left(71^4+71^3+71^2+141\times71+9941\right)+705840\)
\(\Leftrightarrow A=705840\)
27 tháng 8 2017
\(A=x^5-70x^4-70x^3-70x^2-70x+34\)
\(=x^5-71x^4+x^4-71x^3+x^3-71x^2+x^2-71x+x-71+105\)
\(=x^4\left(x-71\right)+x^3\left(x-71\right)+x^2\left(x-71\right)+x\left(x-71\right)+\left(x-71\right)+105\)
\(=\left(x^4+x^3+x^2+x+1\right)\left(x-71\right)+105\)
Thay x = 71\(\Rightarrow A=105\)
Vậy...
18 tháng 9 2021
\(x=71\Leftrightarrow x-1=70\\ \Leftrightarrow A=x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+34\\ A=x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2-x+x+34=34\)
18 tháng 9 2021
\(A=x^5-70x^4-70x^3-70x^2-70x+34\)
\(=x^4\left(x-71\right)+x^3\left(x-71\right)+x^2\left(x-71\right)+x^2\left(x-71\right)+x\left(x-71\right)+x+34\)
\(=x^4\left(71-71\right)+...+x\left(71-71\right)+71+34\)
\(=x^4.0+...+x.0+105=105\)
KB
15 tháng 9 2018
a ) Nếu \(x=71\) \(\Rightarrow70=x-1\)
Thay \(70=x-1\) vào A , ta được :
\(A=x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x\)
\(=x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x\)
\(=x\)
\(=71\)
Vậy \(A=71\) tại \(x=71\)
b ) Ta có : \(x=35\)
\(\Rightarrow\left\{{}\begin{matrix}36=x+1\\37=x+2\\69=2x-1\\34=x-1\end{matrix}\right.\) ( * )
Thay ( * ) vào B , ta được :
\(B=x^5-\left(x+1\right)x^4+\left(x+2\right)x^3-\left(2x-1\right)x^2-\left(x-1\right)x+15\)
\(=x^5-x^5-x^4+x^4+2x^3-2x^3+x^2-x^2+x+15\)
\(=x+15\)
\(=35+15=50\)
Vậy \(B=50\) tại \(x=35\)
ND
1
T
29 tháng 8 2018
A=x5-70x4-70x3-70x2-70x+34 taị x=71
x=71⇒ x-1=71-1=70
A=x5- (x-1)x4 - (x-1)x3-(x-1)x2-(x-1)x + 34
A= x5- x5 + x4 - x4 + x3 - x3 + x2 - x2 + x + 34
A= x + 34⇒71+34=105
CHÚC BẠN HỌC TỐT ^.^