
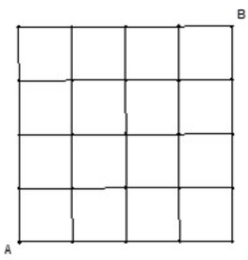
Quan sát hình dưới đây và chỉ ra ít nhất hai cách, để một con kiến bò từ A đến B theo đường chéo của các hình vuông nhỏ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đây là bài toán gì mà mik đọc mãi ko hiểu đề bạn ạk !!!!
xin lỗi nha, mik ko lm đc

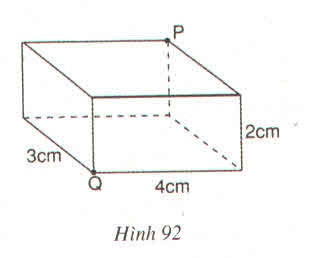
Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
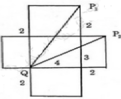
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.


A. Cho đến khi gặp nhau lần thứ nhất ở C:
Kiến đen bò được quãng đường AC, kiến đỏ bò được quãng đường BC, cả 2 con kiến đã bò được 1 lần quãng đường là AC + CB = AB
B. Cho đến khi gặp nhau lần thứ 2 ở D, kiến đen bò được quãng đường là AC + CB + BD = AB + BD, kiến đỏ bò được quãng đường là AB + BD + AB + AD = 3 * AB
C. Khi gặp nhau lần thứ 1 ở C cả 2 con kiến bò được 1 lần quãng đường AB và kiến bò được 7m.
Vậy khi 2 con kiến bò được 3 lần quãng đường AB và gặp nhau ở D thì kiến đen bò được 7m * 3 = 21m.
Hay AB + BD = 21m
AB = 21 - BD
AB = 21- 3
AB = 18m

a) Trắc bách diệp và vạn tuế.
- Cây trắc bách diệp thân cao, dài và rễ cắm vào đất.
- Cây vạn tuê thân nhỏ, thấp hơn và rễ trong chậu
b) Kơ-nia và cau
- Cây Kơ-nia thân to và dài, cành lá xum xuê
- Cây cau thân nhỏ và thon
c) Khế và hoa hồng
- Cây hoa hồng thân mềm, nhỏ
- Cây khế thân to, dài có mọc quả.

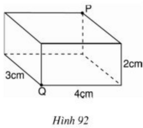
Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.



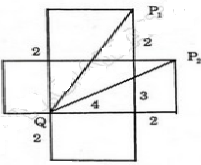

Cách 1:
Cách 2:
Cách 3: