Cho tam giác ABC vg ở B. Gọi K là hình chiếu của B lên AC a) Giả sử AB=6cm, BC=8cm. Tính độ dài các cạnh BK, AK, CK b) Trên tỉa đối của tỉa BC , lấy điểm M sao cho MAC= 90°. CM: CA.KA=CB.BM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

1 tháng 7 2023
a: BC=căn 6^2+8^2=10cm
b: Xét ΔCEB có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCEB cân tại C
mà CA là đường cao
nên CA là phân giác của góc BCE
c: ΔABC vuông tại A có AN là trung tuyến
nên AN=BC/2=5cm
Xét ΔABC có
AN,BM là trung tuyến
AN cắt BM tại K
=>K là trọng tâm
=>AK=2/3AN=10/3(cm)

26 tháng 2 2023
a: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
b: Xet ΔABC có HK//BC
nên AH/AB=HK/BC
=>HK/18=6/9=2/3
=>HK=12(cm)
c: Xét ΔABM có HI//BM
nên HI/BM=AI/AM
Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
=>HI/BM=IK/MC
mà BM=CM
nên HI=IK
=>I là trung điểm của HK

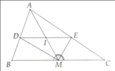


a: ΔCBA vuông tại B
=>\(CA^2=BA^2+BC^2\)
=>\(CA^2=6^2+8^2=100\)
=>CA=10(cm)
Xét ΔCBA vuông tại B có BK là đường cao
nên \(BK\cdot AC=BA\cdot BC\)
=>\(BK\cdot10=6\cdot8=48\)
=>BK=48/10=4,8(cm)
Xét ΔCBA vuông tại B có BK là đường cao
nên \(\left\{{}\begin{matrix}AK\cdot AC=AB^2\left(2\right)\\CK\cdot CA=CB^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AK\cdot10=6^2=36\\CK\cdot10=8^2=64\end{matrix}\right.\)
=>AK=36/10=3,6(cm); CK=64/10=6,4(cm)
b: Xét ΔCAM vuông tại A có AB là đường cao
nên \(CB\cdot BM=BA^2\left(1\right)\)
Từ (1) và (2) suy ra \(CB\cdot BM=CA\cdot KA\)