Cho tam giác ABC có đường cao AH. Gọi I là trung điểm AC, trên tia đối của IH lấy điểm E sao cho IE = IH. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.a) Cm tứ giác AHCE là hình chữ nhật.b) Cm HG= GK= KE.giup mikk...
Đọc tiếp
Cho tam giác ABC có đường cao AH. Gọi I là trung điểm AC, trên tia đối của IH lấy điểm E sao cho IE = IH. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Cm tứ giác AHCE là hình chữ nhật.
b) Cm HG= GK= KE.
giup mikk voiii
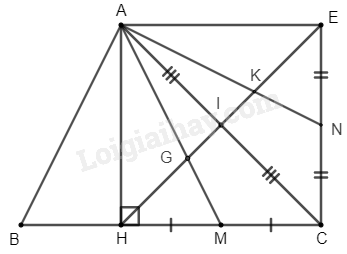
a: Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
b: Xét ΔAHC có
HI,AM là đường trung tuyến
HI cắt AM tại G
Do đó: G là trọng tâm của ΔAHC
=>\(HG=\dfrac{2}{3}HI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot HE=\dfrac{1}{3}HE\)
Xét ΔEAC có
AN,EI là đường trung tuyến
AN cắt EI tại K
Do đó: K là trọng tâm của ΔEAC
=>\(EK=\dfrac{2}{3}EI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot EH=\dfrac{1}{3}EH\)
HG+GK+KE=HE
=>\(GK+\dfrac{1}{3}HE+\dfrac{1}{3}HE=HE\)
=>\(GK=HE\left(1-\dfrac{1}{3}-\dfrac{1}{3}\right)=\dfrac{1}{3}HE\)
=>HG=GK=KE