Trong bài toán mở đầu, hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ

Tóm tắt
\(F=10000N\)
\(t=1p=60s\)
\(h=750m\)
_____________
\(A=?J\)
\(P\left(hoa\right)=?W\)
Giải
Vì máy bay bay lên trực tiếp nên \(h=s=750m\)
Công của động cơ là:
\(A=F.s=10000.750=7500000J\)
Công suất của động cơ là:
\(P\left(hoa\right)=\dfrac{A}{t}=\dfrac{7500000}{60}=125000W\)

đổi 2 giờ 30 phút = 2,5 giờ
vận tốc trực thăng khi ko có gió là :
100 - 5 = 95 ( km/giờ )
vận tốc của máy bay khi ngược gió là :
95 - 5 = 90 ( km/giờ )
máy bay đi đc quãng đường trong 2,5 giờ là :
90 nhân 2,5 = 225 ( km )
Đáp số : 225 km
học tốt mn nha !
đổi 2 giờ 30 p= 2,5 giờ
tốc độ của máy bay trực thăng khi đi ngược chiều gió là:
95-5=90 (km/h)
khi máy báy đi ngược chiều gió trong 2 giờ 30 phút thì đi được số km là
90x2,5=225(km)
Đ/s: 225 km

a) Máy bay đến sân bay Đà Nẵng ứng với thời gian t (giờ) thỏa mãn:
\(\left\{ \begin{array}{l}16,1 = 21,2 - \frac{{153}}{{40}}t\\108,2 = 105,8 + \frac{9}{5}t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{153}}{{40}}t = 5,1\\\frac{9}{5}t = 2,4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = \frac{4}{3}\\t = \frac{4}{3}\end{array} \right. \Leftrightarrow t = \frac{4}{3}\).
Chuyến bay từ Hà Nội đến Đà Nẵng mất \(\frac{4}{3}\) giờ.
b) Tại thời điểm \(t = 1\) giờ, ta có \(x = 21,2 - \frac{{153}}{{40}}.1 = 17,375\)
Vậy tại thời điểm 1 giờ sau khi cất cánh , máy bay ở vị trí có vĩ độ \(17,{375^o}\) Bắc nên máy bay đã bay qua vĩ tuyến 17.

Công của động cơ máy bay là:
\(A=F\cdot s=12000\cdot420=5040000J\)
Công suất của động cơ máy bay là:
\(P=\dfrac{A}{t}=\dfrac{5040000}{90}=5600W\)
Công suất máy bay sinh ra là :
\(A=F.h=12 000.420=5 040 000(J)\)
Công suất của máy bay là:
\(P=\dfrac{A}{t}=\dfrac{5 040 000}{90}=56 000(W)\)

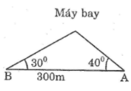
Gọi C là vị trí của máy bay.
Kẻ CH ⊥ AB
Trong tam giác vuông ACH, ta có:
AH = CH.cotgA (1)
Trong tam giác vuông BCH, ta có:
BH = CH.cotgB (2)
Từ (1) và (2) suy ra: (AH + BH) = CH.cotgA + CH.cotgB
Suy ra: CH = 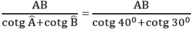 ≈ 102,606 (cm)
≈ 102,606 (cm)

Sau khi xuất phát được 2 giờ tức là máy bay đi được \(\frac{2}{3}\) quãng đường thì ta có máy bay ở điểm M hay là ta có \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} \)
Tọa độ vectơ \(\overrightarrow {AB} = \left( { - 300;400} \right) \Rightarrow \overrightarrow {AM} = \left( { - 200;\frac{{800}}{3}} \right) \Rightarrow \overrightarrow {OM} = \overrightarrow {AM} - \overrightarrow {AO} = \left( { - 600;\frac{{650}}{3}} \right)\)
Vậy tọa độ máy bay sau 2 giờ xuất phát là: \(\left( { - 600;\frac{{650}}{3}} \right)\)