Trong một giải bóng bàn đôi nam, mỗi đội 8 người chọn 2 vận động viên để tạo thành một cặp đấu.
Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Ba cách chọn cặp đấu sẽ là:
+) Cách 1: Chọn Mạnh và Phong
+) Cách 2: Chọn Cường và Tiến
+) Cách 3: Chọn Phong và Cường
b) Mỗi cặp đấu gồm có 2 người nên mỗi cặp đấu là một tập con gồm 2 phần tử được lấy ra từ tập hợp gồm 4 bạn nói trên.
6 tháng 4 2022
+ Tất cả các vận động viên ở trong một phòng. Một vận động viên dẫn tất cả những vận động viên thua anh ta ra ngoài (có thể không dẫn ai – anh ta chỉ ra một mình). Nếu trong phòng còn người thì một vận động viên nào đó lại làm như vừa nêu… Sự việc được tiếp diễn như vậy cho tới khi trong phòng không còn ai hoặc chỉ còn một người. Vận động viên ở vai trò người dẫn là người thắng những vận động viên anh ta dẫn ra và cả những người ở vai trò người dẫn ra trước đó.
=> Nếu trong phòng không còn ai thì người dẫn cuối cùng thoả mãn bài toán.
L
27 tháng 5 2018
Gọi x,y lần lượt là số học sinh nam và nữ của lớp 9A
Điều kiện: x,y>0; x,y nguyên
\(\frac{1}{2}\)số học sinh nam của lớp 9A là \(\frac{1}{2}x\)(học sinh)
\(\frac{5}{8}\)số học sinh nữ của lớp 9A là \(\frac{5}{8}y\)(học sinh)
Tổng số học sinh của lớp 9A là: \(\left(\frac{1}{2}x+\frac{5}{8}y\right)\)học sinh
để tham gia các cặp thi đấu thì số hộc sinh nam phải bằng số học sinh nữ nên ta có: \(\frac{1}{2}x=\frac{5}{8}y\)(1)
Số học sinh còn lại của lớp 9A là 16 học sinh nên:\(\left(x+y\right)-\left(\frac{1}{2}x+\frac{5}{8}y\right)=16\) (2)
Từ (1) và (2) ta có hệ phương trình\(\hept{\begin{cases}\frac{1}{2}x=\frac{5}{8}y\\\left(x+y\right)-\left(\frac{1}{2}x+\frac{5}{8}y\right)=16\end{cases}}\Rightarrow\hept{\begin{cases}x=20\\y=16\end{cases}}\)
Vậy lớp 9A có tất cả 36 học sinh
21 tháng 3 2021
Gọi x,y lần lượt là số học sinh nam và nữ của lớp 9A
Điều kiện: x,y>0; x,y nguyên
số học sinh nam của lớp 9A là (học sinh)
số học sinh nữ của lớp 9A là (học sinh)
Tổng số học sinh của lớp 9A là: học sinh
để tham gia các cặp thi đấu thì số hộc sinh nam phải bằng số học sinh nữ nên ta có: (1)
Số học sinh còn lại của lớp 9A là 16 học sinh nên: (2)
Từ (1) và (2) ta có hệ phương trình
Vậy lớp 9A có tất cả 36 học sinh
14 tháng 4 2020
Có 6 vận động viên cùng đấu ,còn vận động viên còn lại đấu 1 trong 6 người còn lại .Vậy là ai cũng có 1 trận.
Nếu như là 2 trận trở lên thì 1 người phải thi với 2 người trong số họ .
3,4 ,5,6 thì cũng vậy .
Do đó ,trong suốt thời gian thi đấu thì luôn tồn tai 2 vận động viên có số trận như nhau.
CM
4 tháng 5 2017
Đáp án B
Số phần tử của không gian mẫu là: 
Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: 
Vậy xác suất cần tính
CM
16 tháng 9 2017
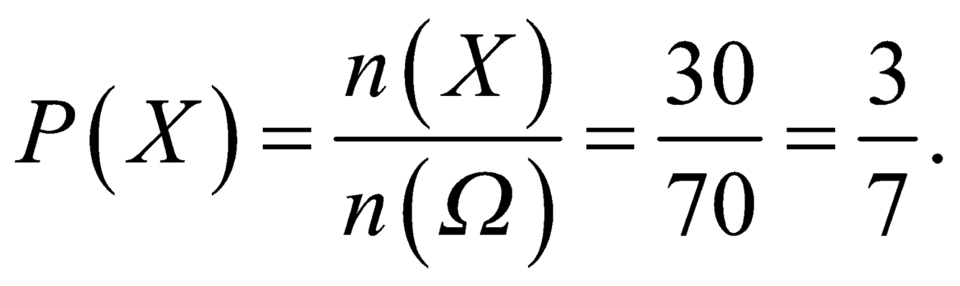
Số phần tử của không gian mẫu là: n Ω = C 8 4 = 70
Gọi X là biến cố: “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: n X = C 2 1 C 2 6 = 30
Vậy xác suất cần tính P X = n X n Ω = 30 70 = 3 7
Đáp án B
YN
27 tháng 5 2021
\(\text{Đội một có số vận động viên là:}\)
\(160.25\%=40\text{ ( vận động viên )}\)
\(\text{Đội hai có số vận động viên là:}\)
\(40:\frac{2}{3}=60\text{ ( vận động viên )}\)
\(\text{Đội ba có số vận động viên là: }\)
\(160-\left(40+60\right)=60\text{ ( vận động viên )}\)
Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.