Vẽ đồ thị các hàm số bậc hai sau:
a) \(y = - {x^2} + 4x - 3\)
b) \(y = {x^2} + 2\)
c) \(y = \frac{1}{2}{x^2} + x + 1\)
d) \(y = {x^2} - 4x + 4\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

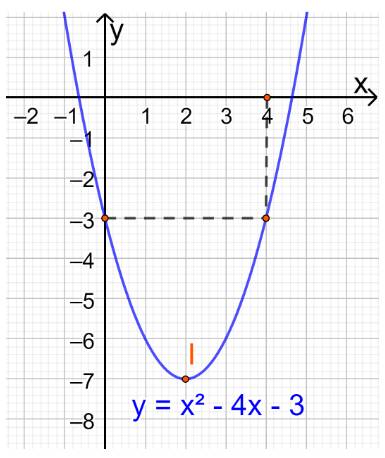
a) Đồ thị hàm số có đỉnh \(I\left( {2; - 7} \right)\)
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
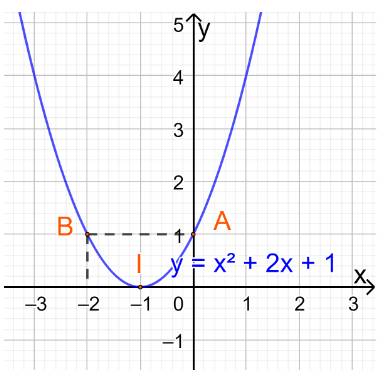
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\)
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
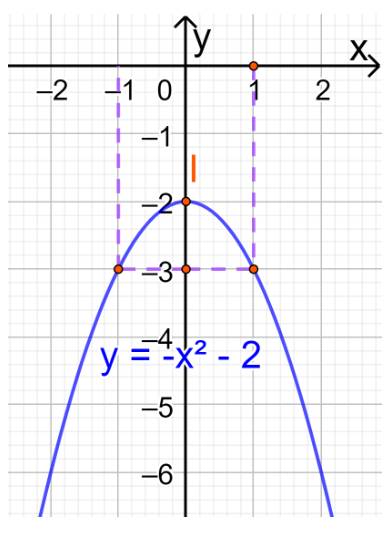
c) Đồ thị hàm số có đỉnh \(I\left( {0; - 2} \right)\)
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

Tham khảo:
a)
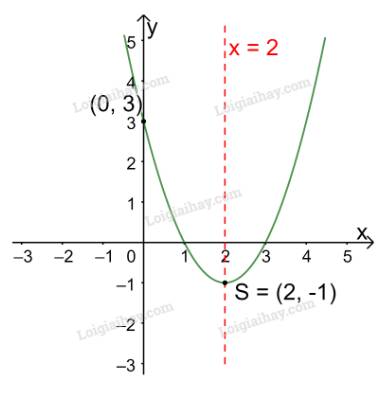
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
b)
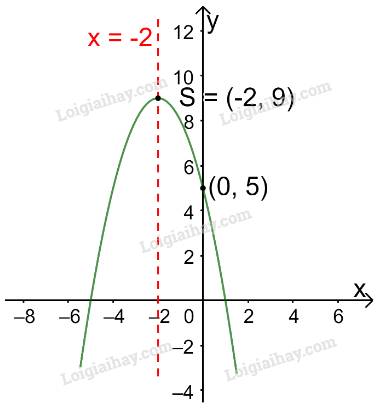
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} = - 2;{y_S} = - {( - 2)^2} - 4.( - 2) + 5 = 9.\)
+ Có trục đối xứng là đường thẳng \(x = - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
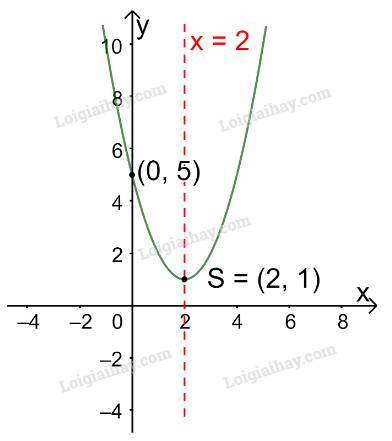
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
d)
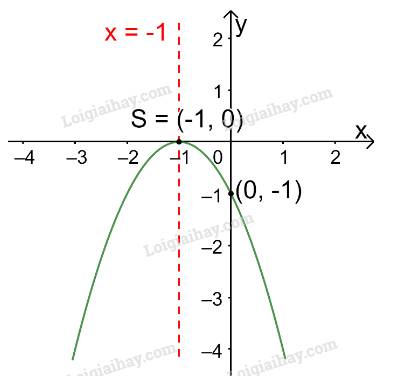
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 2x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} = - 1;{y_S} = - {( - 1)^2} - 2.( - 1) - 1 = 0\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.

Tham khảo:
a)
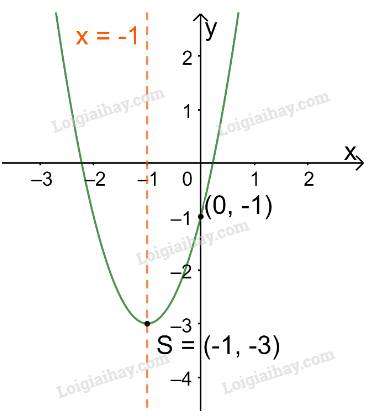
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.

c)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
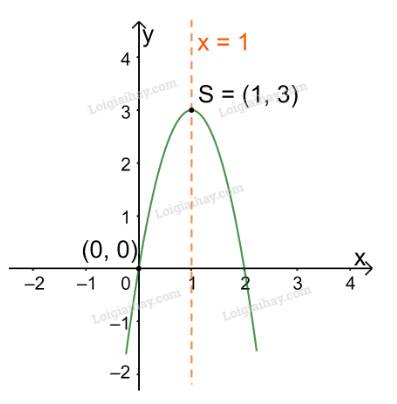
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.


Tham khảo:
a) \(y = {x^2} - 3x - 4\)
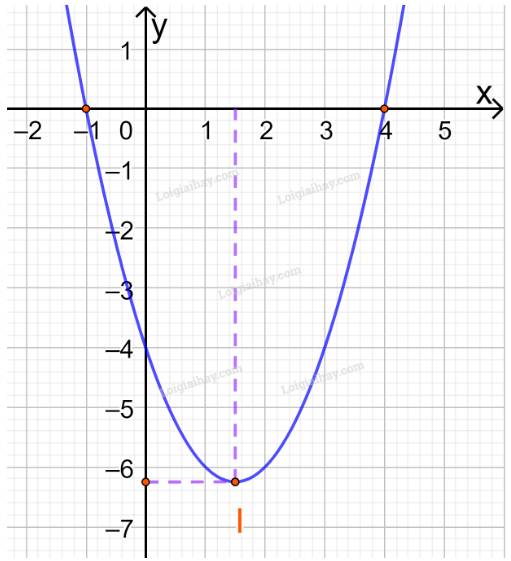
Đồ thị hàm số có đỉnh \(I\left( {\dfrac{3}{2}; - \dfrac{{25}}{4}} \right)\)
Trục đối xứng là \(x = \dfrac{3}{2}\)
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng \(x = \frac{3}{2}\) là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
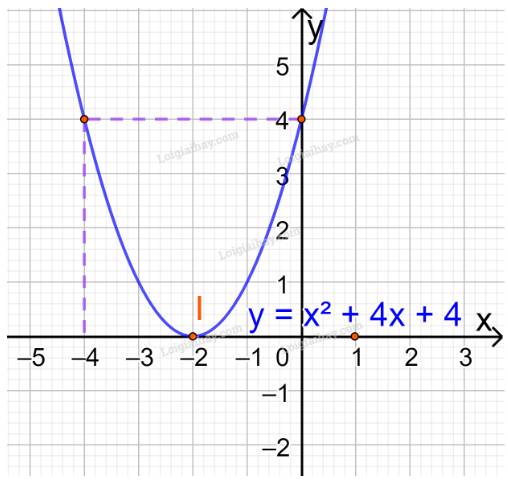
b) \(y = {x^2} + 4x + 4\)
Đồ thị hàm số có đỉnh \(I\left( { - 2;0} \right)\)
Trục đối xứng là \(x = - 2\)
Giao điểm của parabol với trục tung là (0;4)
Giao điểm của parabol với trục hoành là I(-2;0)
Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = - 2\) là (-4;4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
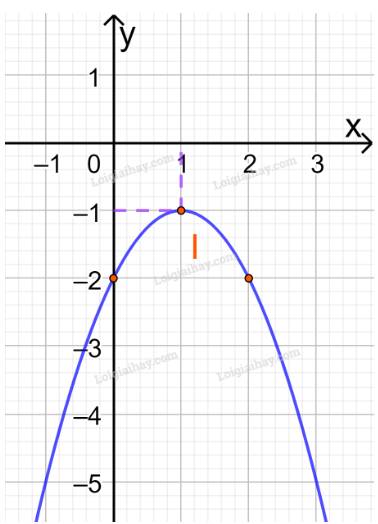
c) \(y = - {x^2} + 2x - 2\)
Đồ thị hàm số có đỉnh \(I\left( {1; - 1} \right)\)
Trục đối xứng là \(x = 1\)
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng \(x = 1\) là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:

`a)TXĐ:R\\{1;1/3}`
`y'=[-4(6x-4)]/[(3x^2-4x+1)^5]`
`b)TXĐ:R`
`y'=2x. 3^[x^2-1] ln 3-e^[-x+1]`
`c)TXĐ: (4;+oo)`
`y'=[2x-4]/[x^2-4x]+2/[(2x-1).ln 3]`
`d)TXĐ:(0;+oo)`
`y'=ln x+2/[(x+1)^2].2^[[x-1]/[x+1]].ln 2`
`e)TXĐ:(-oo;-1)uu(1;+oo)`
`y'=-7x^[-8]-[2x]/[x^2-1]`
Lời giải:
a.
$y'=-4(3x^2-4x+1)^{-5}(3x^2-4x+1)'$
$=-4(3x^2-4x+1)^{-5}(6x-4)$
$=-8(3x-2)(3x^2-4x+1)^{-5}$
b.
$y'=(3^{x^2-1})'+(e^{-x+1})'$
$=(x^2-1)'3^{x^2-1}\ln 3 + (-x+1)'e^{-x+1}$
$=2x.3^{x^2-1}.\ln 3 -e^{-x+1}$
c.
$y'=\frac{(x^2-4x)'}{x^2-4x}+\frac{(2x-1)'}{(2x-1)\ln 3}$
$=\frac{2x-4}{x^2-4x}+\frac{2}{(2x-1)\ln 3}$
d.
\(y'=(x\ln x)'+(2^{\frac{x-1}{x+1}})'=x(\ln x)'+x'\ln x+(\frac{x-1}{x+1})'.2^{\frac{x-1}{x+1}}\ln 2\)
\(=x.\frac{1}{x}+\ln x+\frac{2}{(x+1)^2}.2^{\frac{x-1}{x+1}}\ln 2\\ =1+\ln x+\frac{2^{\frac{2x}{x+1}}\ln 2}{(x+1)^2}\)
e.
\(y'=-7x^{-8}-\frac{(x^2-1)'}{x^2-1}=-7x^{-8}-\frac{2x}{x^2-1}\)

`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
câu l) $x^2-1 > 0$ thì giải ra 2 nghiệm $x < -1, x > 1$ mới đúng chứ nhỉ?

a: 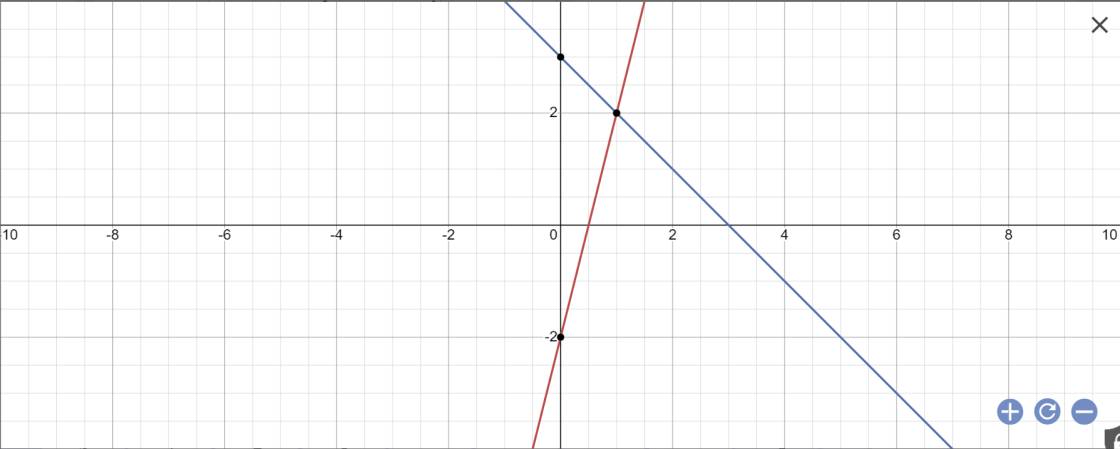
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)
a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
Ta có ngay parabol trên vùng làm việc như hình dưới:
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
Ta có ngay parabol trên vùng làm việc như hình dưới:
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
Ta có ngay parabol trên vùng làm việc như hình dưới: