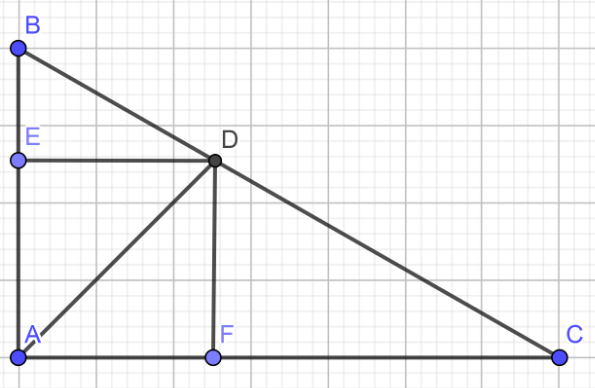
cho tam giác ABC vuông tại A, đường phân giác AD. Gọi E, F lần lượt là hình chiếu của D trên AB, AC. Biết BD = 3, DC = 4. Chứng minh rằng: AEDF là hình vuông và tính diện tích của nó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác AEDF có
góc AED=góc ADF=góc EAD=90 độ
=>AEDF là hình chữ nhật
mà AD là phân giác của góc FAE
nên AEDF là hình vuông

Bài 5:
Xét ΔABC vuông tại A
Áp dụng Pytago ta có:
BC2 = AB2 + AC2
= 242 + 322
⇒ BC = 40
DE là trung trực của BC
⇒ E là trung điểm của BC; DE vuông góc với BC tại E
⇒ EC = BC/2 = 40/2 = 20
Xét ΔCED và ΔCAB có:
∠CED = ∠CAB = 90o
∠C chung
⇒ ΔCED đồng dạng ΔCAB
⇒ CE/CA = ED/AB
⇒ 12/32 = ED/24
⇒ ED = 9

Theo tính chất đường phân giác ta có:\(\frac{AB}{AC}=\frac{BD}{CD}=\frac{2}{3}\Rightarrow AB=\frac{2}{3}AC\)
Áp dụng định lí Pitago vào tam giác vuông ABC ta tính được;\(AC^2+AB^2=BC^2\Leftrightarrow\frac{4}{9}AC^2+AC^2=5^2\)
\(\Rightarrow AC=\frac{15\sqrt{13}}{13}cm;AB=\frac{10\sqrt{13}}{13}cm\)
Ta lại có \(\Delta FDC\)đồng dạng \(\Delta EBD\left(góc-góc\right)\)
\(\Rightarrow\frac{FD}{EB}=\frac{FC}{ED}=\frac{DC}{BD}=\frac{3}{2}\)
\(\Rightarrow EB=\frac{2}{3}FD;FC=\frac{3}{2}ED\)
Vì AD là tia phân giác của góc vuông=> Các Tam giác AED và AFD là tam giác vuông cân => Tứ giác AEDF là hình vuông.
Gọi cạnh hình vuông AEDF là x hay AE=AF=FD=ED=x
\(VìAE=AF\Rightarrow AB-EB=AC-FC\)
\(AB-\frac{2}{3}FD=AC-\frac{3}{2}ED\)
\(\frac{10\sqrt{13}}{13}-\frac{2}{3}x=\frac{15\sqrt{13}}{13}-\frac{3}{2}x\)
\(\frac{5x}{6}=\frac{5\sqrt{13}}{13}\Rightarrow x=\frac{6\sqrt{13}}{13}cm\)
diện tích hình tam giác ABC \(S_{\Delta ABC}=\frac{1}{2}AB.AC=\frac{75}{13}cm^2\)
diện tích hình vuông AEDF:\(S_{AEDF}=x^2=\frac{36}{13}cm^2\)
Tổng diện tích tam giác DEB và DFC\(S=\frac{75}{13}-\frac{36}{13}=3cm^2\)
Hình mình vẽ chưa chính xác lắm, bạn vẽ lại nhe. chúc bạn học tốt
Cảm ơn bạn Trường An nhiều nhé. Chúc bạn luôn may mắn, thành công.

\(a,BC=\sqrt{AB^2+AC^2}=15\left(cm\right)\left(pytago\right)\)
\(b,\) Áp dụng HTL: \(AH\cdot BC=AB\cdot AC\Leftrightarrow AH=\dfrac{9\cdot12}{15}=7,2\left(cm\right)\)
\(c,\) Dễ thấy AEHF là hcn
Do đó \(\widehat{HAF}=\widehat{EFA}\)
Mà \(\widehat{HAF}=\widehat{HBA}\left(cùng.phụ.\widehat{HAB}\right)\)
Do đó \(\widehat{EFA}=\widehat{HBA}\)
Ta có \(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{EFA}\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AEF\sim\Delta ACB\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AC}=\dfrac{AF}{AB}\Rightarrow AE\cdot AB=AF\cdot AC\)
\(d,\) Áp dụng HTL: \(\left\{{}\begin{matrix}AH^2=EA\cdot AB\\AH^2=FA\cdot AC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AE=\dfrac{AH^2}{AB}=5,76\left(cm\right)\\AF=\dfrac{AH^2}{AC}=4,32\left(cm\right)\end{matrix}\right.\)
\(\Rightarrow S_{AEF}=\dfrac{1}{2}AE\cdot AF=\dfrac{1}{2}\cdot5,76\cdot4,32=12,4416\left(cm^2\right)\)
Mà \(S_{ABC}=\dfrac{1}{2}AB\cdot AC=54\left(cm^2\right)\)
Vậy \(S_{BEFC}=S_{ABC}-S_{AEF}54-12,4416=41,5584\left(cm^2\right)\)