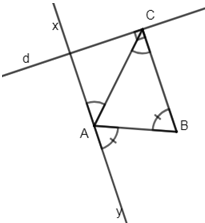
Cho \(\Delta ABC\) nhọn. Lấy I bất kì trên BC. Trên nửa mặt phẳng bờ BC không chứa diểm A vẽ Cx sao cho \(\widehat{BCx}=\widehat{BAI}\). AI cắt Cx tại D.
a) C/m: \(\widehat{BAC}+\widehat{BDC}=180\)độ
b) Kẻ \(DH⊥BC;DK⊥AC\) .
C/m: \(\widehat{KHC}=\widehat{KDC}\)
c) Kẻ \(DL⊥AB\)
C/m: \(\widehat{BDL}=\widehat{CDK}\)
d) C/m: K,H,L thẳng hàng