Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình...
Đọc tiếp
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
H
2
Những câu hỏi liên quan
15 tháng 9 2021
1: \(100-x^2=\left(10-x\right)\left(10+x\right)\)
2: \(b^2-a^2=\left(b-a\right)\left(b+a\right)\)
3: \(\left(3y\right)^2-\left(4x\right)^2=\left(3y-4x\right)\left(3y+4x\right)\)
N
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
6.B
Hàm nghịch biến trên R khi:
\(1-m< 0\Rightarrow m>1\)
5.B
Đồ thị đi qua A nên:
\(-1=2a-2\Rightarrow2a=1\Rightarrow a=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
\(x^2+2x+2=\left(x+1\right)^2+1>0;\forall x\in R\)
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
\(3m+2=3+2m\Rightarrow m=1\)
TN
2 tháng 11 2021
10D.
Hai đường thẳng (D) và (D') cùng đi qua điểm (0;-2) nên chúng không bao giờ song song nhau
11.A
x2+2x+2=(x+1)2+1>0;∀x∈Rx2+2x+2=(x+1)2+1>0;∀x∈R
12.C
Hai đồ thị cắt nhau tại 1 điểm trên trục tung khi:
3m+2=3+2m⇒m=1
2 tháng 8 2017
x+√(x^2+3)=3/(y+√(y^3))=3(y-√(y^2+3)/-a(trục căn thức)
x+√(x^2+3)=-y+√(y^2+3) suy ra x+y=√(y^2+3)-√(x^2+3)(1)
Tương tự,x+y=√(x^2+3)-√(y^2+3)(2)
Cộng (1),(2) theo vế suy ra 2(x+y)=0 suy ra x+y=0
hay E=0.
Vậy E=0
2 tháng 8 2017
nhân \(-x+\sqrt{x^2+3}\) vào 2 vế ta đc : \(\left(-x^2+x^2+3\right)\left(y+\sqrt{y^2+3}\right)=\)\(3\left(-x+\sqrt{x^2+3}\right)\)
<=> \(y+\sqrt{y^2+3}=-x+\sqrt{x^2+3}\)<=> \(y+\sqrt{y^2+3}+x-\sqrt{x^2+3}=0\)__(1)___
làm tương tự ta đc \(\left(-y+\sqrt{y^2+3}\right)\left(x+\sqrt{x^2+3}\right)\)\(=3\left(-y+\sqrt{y^2+3}\right)\)
<=> \(x+\sqrt{x^2+3}=-y+\sqrt{y^2+3}\)<=> \(x+\sqrt{x^2+3}+y-\sqrt{y^2+3}=0\)__(2)__
lấy (1) + (2) => 2(x+y) =0 => x+y=0
lấy
LN
2
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)
LT
5 tháng 9 2015
bài này có nhiều cách hợp lý , vậy tìm 1 cách hay tất cả các cách
F
1
AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
a.
Diện tích mảnh đất là: $12.10=120$ (m2)
Diện tích phần đất trồng hoa: $6.8=48$ (m2)
b.
Diện tích trồng cỏ là: $120-48=72$ (m2)
Tổng tiền công chi trả để trồng hoa và cỏ là:
$48.40 000 +72.30 000=4080000$ (đồng)
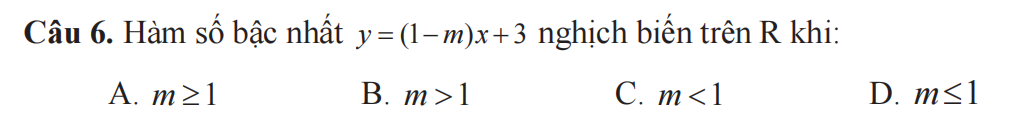
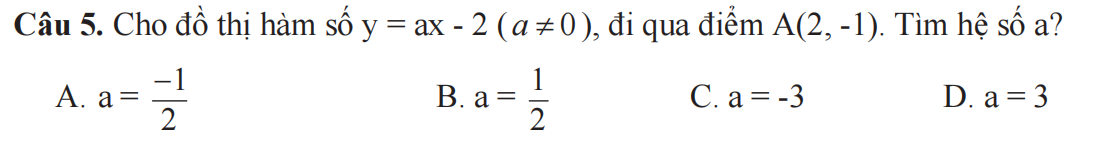
\(2\left(x-3\right)^4-3^2=503\\ \Rightarrow2\left(x-3\right)^4=512\\ \Rightarrow\left(x-3\right)^4=256\\ \Rightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
`2(x-3)^4-3^2=503`
`=>2(x-3)^4-9=503`
`=>2(x-3)^4=503+9`
`=>2(x-3)^4=512`
`=>(x-3)^4=512:2`
`=>(x-3)^4=256`
`=>(x-3)^4=4^4` hoặc `(x-3)^4=(-4)^4`
`=>x-3=4` hoặc `x-3=-4`
`=>x=7` hoặc `x=-1`
Vậy `x in{-1;7}`