Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đề bài đề bài sai rồi đề bài đúng là tìm 2 số có tỉ số bằng 3 biết nếu bớt ở số thứ nhất và thêm 10 ở số thứ hai ta được hai số mới có tỉ số là 5/3 chứ
\(\frac{a}{b}\)=\(\frac{3}{1}\)vậy \(\frac{a}{a+b}\)=\(\frac{3}{4}\)
\(\frac{a-10}{b+10}\)=\(\frac{5}{3}\)vậy \(\frac{a-10}{a+b}\)=\(\frac{5}{8}\)
ta thấy \(\frac{3}{4}\)và\(\frac{3}{8}\)chưa cùng mẫu số ta sẽ quy đồng chúng thành:\(\frac{6}{8}\)và \(\frac{5}{8}\)
ta có sơ đồ:
a :6 phần
a-10:5 phần
hiệu của chúng là:10
a=10*6=60
b=60*3=20
đây là toán nâng cao và a là số số lớn,b là số bé
nhớ học nhiều rồi bài này sẽ dễ

Tổng 2 số là :
1975 + 79 - 54 = 2000
Tổng số phần bằng nhau là :
1 + 4 = 5 ( phần )
Số bé là :
2000 : 5 = 400
Số lớn là :
2000 - 400 = 1600
Đáp số : 400 , 1600

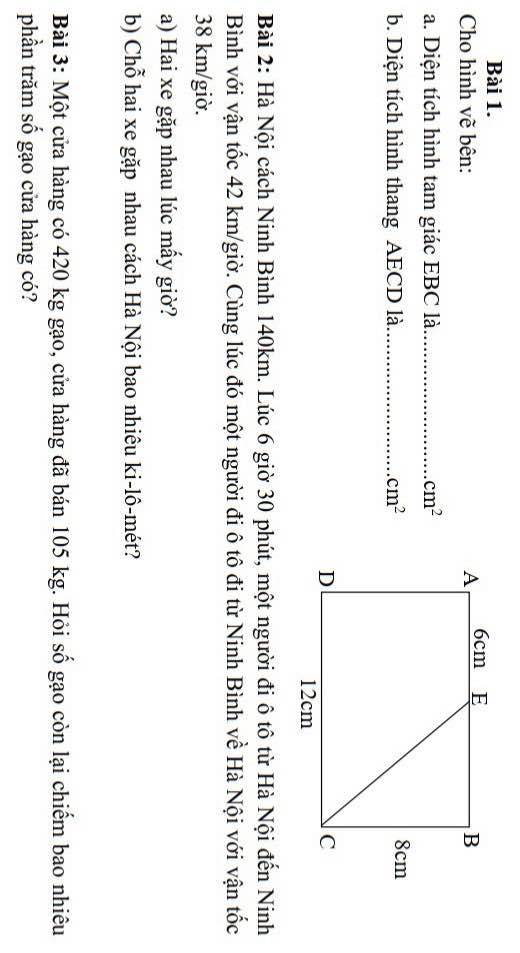
Bài 4.
Gọi 2 số cần tìm lần lượt là a, b.
Theo bài ta có:
a + 2005 + (b - 2468) = 13579 => a + 2005 + b - 2468 = 13579 => a + b = 13579 - 2005 + 2468 => a + b = 14042
Vậy tổng hai số là 14042.
Bài 5.
Gọi số bị trừ và số trừ lần lượt là a, b.
Theo bài ta có:
(a - 2005) - (b - 1357) = 24680 => a - 2005 - b + 1357 = 24680 => a - b = 24680 + 2005 - 1357 => a - b = 25328
Vậy hiệu hai số là 25328.

Đây là toán nâng cao của tiểu học trong kỳ thi cấp huyện trở nên, dạng hai tỉ số tổng không đổi em nhé.
Dưới đây là phương pháp giải của cô. Em tham khảo nhé:
Vì thêm vào số thứ nhất 6 và đồng thời bớt 6 ở số thứ hai nên tổng hai số lúc sau không đổi so với ban đầu.
Số thứ nhất lúc đầu so với tổng hai số chiếm :
3 : ( 3 + 4) = \(\dfrac{3}{7}\) ( tổng hai số)
Số thứ nhất lúc sau so với tổng hai số chiếm:
4 : ( 3 + 4) = \(\dfrac{4}{7}\) ( tổng hai số)
Phân số chỉ 6 đơn vị là:
\(\dfrac{4}{7}\) - \(\dfrac{3}{7}\) = \(\dfrac{1}{7}\) ( tổng hai số)
Tổng hai số là: 6 : \(\dfrac{1}{7}\) = 42
Ta có sơ đồ:

Theo sơ đồ ta có: Số thứ nhất lúc đầu là: 42 : ( 3 + 4) \(\times\) 3 = 18
Số thứ hai lúc đầu là: 42 - 18 = 24
Đáp số: số thứ nhất lúc đầu 18
số thứ hai lúc đầu 24
Gọi số thứ nhất là a, số thứ hai là b
Vì a/b = 3 nên a = 3b
ta có
\(\dfrac{a-10}{b+10}=\dfrac{5}{3}\)
⇔ \(\dfrac{3b-10}{b+10}=\dfrac{5}{3}\)
⇒3(3b-10) = 5(b+10)
⇔ 9b -30 = 5b +50
⇔ 9b - 5b = 50 +30
⇔ 4b = 80
⇔ b = 20
⇒ a = 60