cứu :((tui tick cho
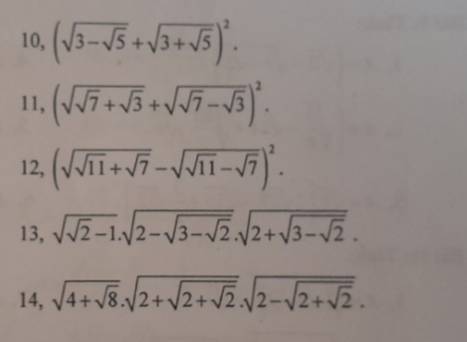
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(A=\sqrt{\dfrac{2}{3}}-\sqrt{24}+2\cdot\sqrt{\dfrac{3}{8}}+\sqrt{\dfrac{1}{6}}\)
\(=\sqrt{\dfrac{6}{9}}-2\sqrt{6}+2\cdot\sqrt{\dfrac{6}{16}}+\sqrt{\dfrac{6}{36}}\)
\(=\dfrac{1}{3}\sqrt{6}-2\sqrt{6}+\dfrac{1}{2}\sqrt{6}+\dfrac{1}{6}\sqrt{6}\)
\(=-\sqrt{6}\)
2: \(A=\sqrt{150}+\sqrt{96}+\dfrac{9}{2}\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}+4\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}-\sqrt{6}\)
\(=8\sqrt{6}+\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=8\sqrt{6}+3\sqrt{3}\cdot\sqrt{2}=11\sqrt{6}\)
3: \(A=2\sqrt{45}+\sqrt{32}-2\sqrt{20}-\dfrac{9}{2}\cdot\sqrt{8}\)
\(=2\cdot3\sqrt{5}+4\sqrt{2}-2\cdot2\sqrt{5}-\dfrac{9}{2}\cdot2\sqrt{2}\)
\(=6\sqrt{5}-4\sqrt{5}+4\sqrt{2}-9\sqrt{2}\)
\(=2\sqrt{5}-5\sqrt{2}\)
4: \(A=\sqrt{75}-\dfrac{1}{2}\cdot\sqrt{48}+\sqrt{300}-\sqrt{147}\)
\(=5\sqrt{3}-\dfrac{1}{2}\cdot4\sqrt{3}+10\sqrt{3}-7\sqrt{3}\)
\(=8\sqrt{3}-2\sqrt{3}=6\sqrt{3}\)
5: \(A=\sqrt{54}+2\sqrt{24}-\dfrac{3}{2}\cdot\sqrt{96}-\sqrt{216}\)
\(=3\sqrt{6}+2\cdot2\sqrt{6}-6\sqrt{6}-\dfrac{3}{2}\cdot4\sqrt{6}\)
\(=-3\sqrt{6}+4\sqrt{6}-6\sqrt{6}\)
\(=-5\sqrt{6}\)
6: \(A=3\sqrt{50}-2\sqrt{75}-4\cdot\dfrac{\sqrt{54}}{\sqrt{3}}-3\sqrt{\dfrac{1}{3}}\)
\(=3\cdot5\sqrt{2}-2\cdot5\sqrt{3}-4\cdot\sqrt{18}-\sqrt{3}\)
\(=15\sqrt{2}-10\sqrt{3}-12\sqrt{2}-\sqrt{3}\)
\(=3\sqrt{2}-11\sqrt{3}\)

12 phút 48 giây = 768
3,4 giờ = 3 giờ 24 phút
5,7 giờ = 5 giờ 42 phút
\(\dfrac{5}{6}\)phút = 50 giây
12 phút 48 giây = 12 phút + \(\dfrac{48}{60}\) phút = 12,8 phút
3,4 giờ = 3 giờ + 60 phút \(\times\) 0,4 = 3 giờ 24 phút
5,7 giờ = 5 giờ + 60 phút \(\times\) 0,7 = 5 giờ 42 phút
\(\dfrac{5}{6}\) phút = \(60\) giây \(\times\) \(\dfrac{5}{6}\) = 50 giây

\(\text{Giải:}\)
\(\text{Gọi x là số sách cần tìm}\left(x\inℕ^∗;100\le x\le200\right)\)
\(\text{Ta có}:x:3\text{dư}1\Rightarrow x+1⋮3\)
\(\text{x:5 dư 1 => x+1 5}\text{x:5 dư 1 => x+1 5}\text{dư}1\Rightarrow x+1⋮5\)
\(x:7\text{dư}1\Rightarrow x+1⋮7\)
\(\text{=> x+1 BC(3,5,7)}\)
\(\text{Ta lại có 3,5,7 nguyên tố cùng nhau từng đôi một}\)
\(\text{=> BCNN(3,5,7) = 3.5.7 = 105}\)
\(\)\(\)\(\)\(\Rightarrow BC\left(3,5,7\right)=B\left(105\right)=\left\{0;105;210;...\right\}\)
\(\Rightarrow x\in\left\{0;105;210;...\right\}\)
\(\text{Mà}100\le x\le200\Rightarrow x=105\)
\(\text{Vậy trường X mua về 105 quyển sách.}\)


Sau đây là gợi ý của mình:
Sau khi tạm biệt Cáo để trở về hành tinh của mình, Hoàng tử bé luôn cảm thấy lưu luyến và hi vọng được gặp người bạn tốt này. Trong hành trinh chinh phục và khám phá Trái đất, Cáo chính là người trao cho cậu sự ấm áp nhất. Nhờ có Cáo, Hoàng tử bé đã nhận ra tình cảm của mình dành cho bông hoa hồng. Thời gian vun trồng chăm sóc bông hoa hồng chính là điều khiến bông hồng ở hành tinh của cậu trở nên "độc nhất vô nhị". Cáo chính là một ngọn đèn soi đường để Hoàng tử bé đến với chân lý và học được cách yêu thương điều quan trọng mà bấy lâu nay bản thân cậu không nhận ra. Cáo là người bạn dù thời gian tiếp xúc thật ngắn ngủi nhưng lại là người khiến cậu không thể nào quên. Cậu tự hứa với lòng nếu còn cơ hội trở lại, nhất định sẽ tìm gặp Cáo. Hai người sẽ đồng hành cùng nhau khám phá các hành tinh trong vũ trụ và dẫn Cáo gặp mặt bông hồng mà cậu yêu nhất ... ( bạn tự viết thêm nha )

Em tách nhỏ ra để hỏi, không đăng cả đề như thế này, em nhé!
10: \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=\left(\sqrt{3-\sqrt{5}}\right)^2+\left(\sqrt{3+\sqrt{5}}\right)^2+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{9-5}\)
\(=6+2\cdot2=10\)
11: \(\left(\sqrt{\sqrt{7}+\sqrt{3}}+\sqrt{\sqrt{7}-\sqrt{3}}\right)^2\)
\(=\left(\sqrt{\sqrt{7}+\sqrt{3}}\right)^2+\left(\sqrt{\sqrt{7}-\sqrt{3}}\right)^2+2\cdot\sqrt{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}\)
\(=\sqrt{7}+\sqrt{3}+\sqrt{7}-\sqrt{3}+2\cdot\sqrt{7-3}\)
\(=2\sqrt{7}+2\cdot2=2\sqrt{7}+4\)
12: \(\left(\sqrt{\sqrt{11}+\sqrt{7}}-\sqrt{\sqrt{11}-\sqrt{7}}\right)^2\)
\(=\left(\sqrt{\sqrt{11}+\sqrt{7}}\right)^2+\left(\sqrt{\sqrt{11}-\sqrt{7}}\right)^2-2\cdot\sqrt{\left(\sqrt{11}-\sqrt{7}\right)\left(\sqrt{11}+\sqrt{7}\right)}\)
\(=\sqrt{11}+\sqrt{7}+\sqrt{11}-\sqrt{7}-2\cdot\sqrt{11-7}\)
\(=2\sqrt{11}-4\)
13:
\(\sqrt{\sqrt{2}-1}\cdot\sqrt{2-\sqrt{3-\sqrt{2}}}\cdot\sqrt{2+\sqrt{3-\sqrt{2}}}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{4-\left(3-\sqrt{2}\right)}\)
\(=\sqrt{\sqrt{2}-1}\cdot\sqrt{\sqrt{2}+1}\)
\(=\sqrt{2-1}=1\)
14:
\(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2+\sqrt{2}}}\cdot\sqrt{2-\sqrt{2+\sqrt{2}}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{\left(2+\sqrt{2+\sqrt{2}}\right)\left(2-\sqrt{2+\sqrt{2}}\right)}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2-\sqrt{2}}\)
\(=\sqrt{\left(4+2\sqrt{2}\right)\left(2-\sqrt{2}\right)}\)
\(=\sqrt{8-4\sqrt{2}+4\sqrt{2}-4}=\sqrt{4}=2\)