Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
Suy ra: MB=AQ
Xét tứ giác AMBQ có
MB//AQ
MB=AQ
Do đó: AMBQ là hình bình hành
mà \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
Câu a có r mk ko ghi lại nx nhe
b) Ta có AQBM là HCN (CMa)
=> ^AQB=900 hay BQ ⊥ AC
=> BQ là đường cao của ΔABC
Mà H là giao điểm của 2 đường cao AI và BQ của ΔABC (gt)
=> H là trực tâm của ΔABC
=> CH cũng là đường cao của ΔABC (H là trực tâm; H ∈ CH)
=> CH ⊥ AB (đpcm)
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)(hai góc so le trong, BM//AC)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)(hai góc đối đỉnh)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
=>P là trung điểm của MQ
Xét tứ giác AMBQ có
P là trung điểm chung của AB và MQ
=>AMBQ là hình bình hành
Hình bình hành AMBQ có \(\widehat{MAQ}=90^0\)
nên AMBQ là hình chữ nhật
b: Ta có: AMBQ là hình chữ nhật
=>BQ\(\perp\)AQ tại Q
=>BQ\(\perp\)AC tại Q
Xét ΔABC có
BQ,AI là các đường cao
BQ cắt AI tại H
Do đó: H là trực tâm của ΔABC
=>CH\(\perp\)AB
c: Ta có: AMBQ là hình chữ nhật
=>AB=QM
mà \(PQ=\dfrac{QM}{2}\)
nên \(PQ=\dfrac{AB}{2}=PA\)(1)
Ta có: ΔAIB vuông tại I
mà IP là đường trung tuyến
nên IP=PA(2)
Từ (1) và (2) suy ra PI=PQ
=>ΔPIQ cân tại P
a: Xét ΔPBM và ΔPAQ có
\(\widehat{PBM}=\widehat{PAC}\)
PB=PA
\(\widehat{BPM}=\widehat{APQ}\)
Do đó: ΔPBM=ΔPAQ
=>PM=PQ
Xét tứ giác AQBM có
P là trung điểm chung của AB và QM
=>AQBM là hình bình hành
=>BQ//AM
=>HQ//AM
=>AQHM là hình thang
a: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
Xét ΔPBQ và ΔPAM có
PB=PA
\(\widehat{BPQ}=\widehat{APM}\)
PQ=PM
Do đó: ΔPBQ=ΔPAM
=>\(\widehat{PBQ}=\widehat{PAM}\)
mà hai góc này là hai góc so le trong
nên BQ//AM
=>HQ//AM
=>AQHM là hình thang
b: Xét tứ giác AMBQ có
AQ//BM
BQ//AM
Do đó: AMBQ là hình bình hành
a,b: Xét ΔPMB và ΔPQA có
\(\widehat{PBM}=\widehat{PAQ}\)
PB=PA
\(\widehat{MPB}=\widehat{QPA}\)
Do đó: ΔPMB=ΔPQA
=>PM=PQ
=>P là trung điểm của MQ
Xét tứ giác AQBM có
P là trung điểm chung của AB và QM
=>AQBM là hình bình hành
=>AM//BQ
=>BQ\(\perp\)AC
Xét tứ giác AQHM có HQ//AM
nên AQHM là hình thang
) HS tự chứng minh AMBQ là hình chữ nhật (ahi đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
b) Sử dụng tính chất trực tâm tam giác.
c) Sử dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh
P I = P Q = 1 2 A B .
Mai pk nộp ròi, giúp tui trog tối nay điiii
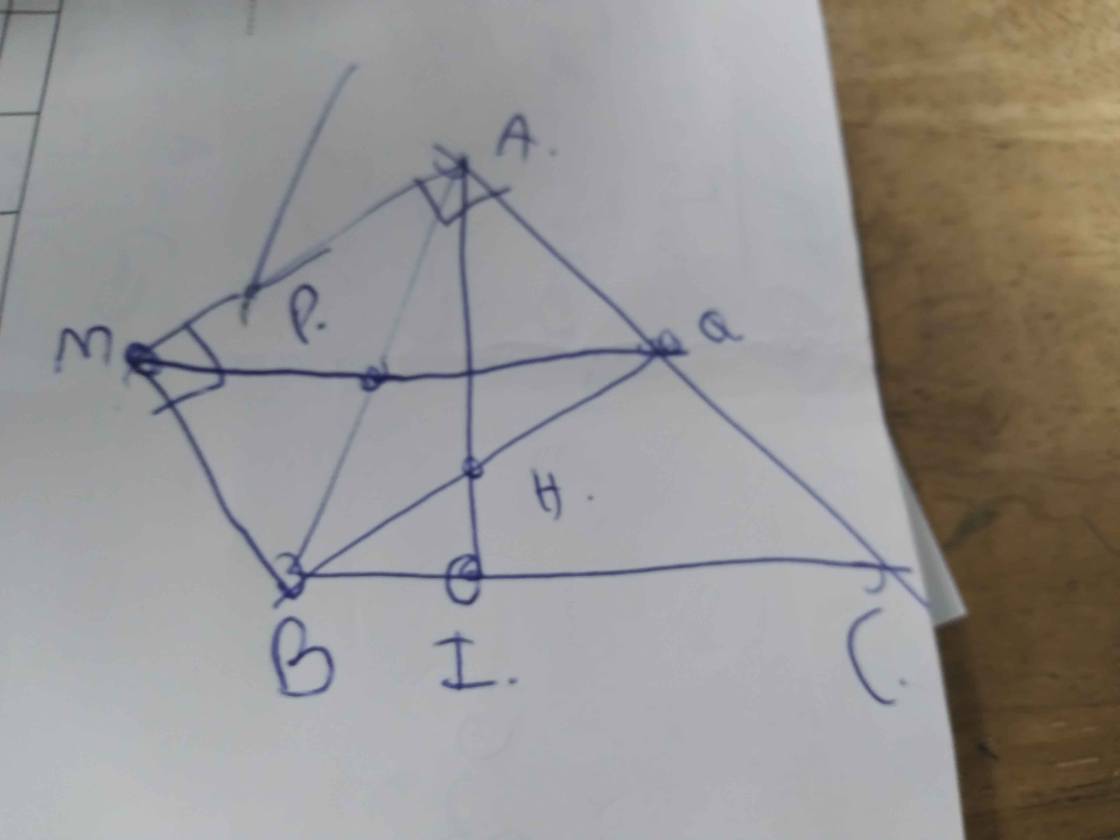
a) Ta có: ��⊥��Ax⊥AC và ��By // ��AC
=> ��⊥��Ax⊥By ⇒���^=90∘
⇒Góc AMB = 90 độ
Xét Δ���ΔMAQ và Δ���ΔQBM có
���^=���^Góc MQA = góc BQM (so le trong);
��MQ là cạnh chung;
���^=���^Góc AMQ = góc BQM(Ax//QB)
Suy ra Δ���= Δ���ΔMAQ= ΔQBM (g-c-g)
Suy ra góc MBQ = góc MAQ= 90 độ (2 góc tương ứng)
Xét tứ giác AMBQ có
Góc QAM = góc AMB = góc MBQ = 90 độ
=> tứ giác ����AMBQ là hình chữ nhật.
b) Do tứ giác ����AMBQ là hình chữ nhật
Mà P là trung điểm AB
=>P là trung điểm của MQ; AB = MQ
=> PQ = 1/2 AB (1)
Xét tam giác AIB vuông tại I và có IP là đường trung tuyến
=> IP = 1/2 AB(2)
Từ (1) và (2)
=> QP =IP
=> Tam giác PQI cân tại P