Cho A = \(\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
B = \(\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
Chứng tỏ rằng A > B.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
12 tháng 5 2021
Lời giải:
\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
NA
Nguyễn An Ninh
VIP
25 tháng 4 2023
b\()\)
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2.3 + 1/3.4 +... + 1/99.100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/3 + 1/3 -1/4 +... + 1/99 + 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 3/4 - 1/100 < 3/4
NA
Nguyễn An Ninh
VIP
25 tháng 4 2023
Tương tự như vậy với câu a\()\)
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2.3 + 1/3.4 +... + 1/99.100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/3 + 1/3 -1/4 +... + 1/99 + 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 3/4 - 1/100 < 1/2
NA
Ngoc Anh Thai
Giáo viên
11 tháng 4 2021
a)
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{30^2}\\ < \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{29.30}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{29}-\dfrac{1}{30}\\ =1-\dfrac{1}{30}=\dfrac{29}{30}< 1\left(dpcm\right)\)
b)
\(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}=\dfrac{1}{10}+\left(\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)\\ >\dfrac{1}{10}+\dfrac{1}{100}+\dfrac{1}{100}+...+\dfrac{1}{100}=\dfrac{1}{10}+\dfrac{90}{100}\\ =\dfrac{110}{100}>1\left(đpcm\right).\)
NA
Ngoc Anh Thai
Giáo viên
11 tháng 4 2021
c)
\(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}\\ =\left(\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{9}\right)+\left(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{17}\right)\\ < \dfrac{1}{5}.5+\dfrac{1}{8}.8=1+1=2\left(đpcm\right)\)
d) tương tự câu 1
DT
Đỗ Thanh Hải
CTVVIP
2 tháng 5 2021
Ta có
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)
...............
\(\dfrac{1}{8^2}< \dfrac{1}{7.8}\)
=> B < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+....+\dfrac{1}{7.8}\)
B < \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
B < \(1-\dfrac{1}{8}< 1\) (Do \(\dfrac{1}{8}>0\))
Vậy.....
20 tháng 4 2021
a) Ta có: \(A=\dfrac{4}{7\cdot31}+\dfrac{6}{7\cdot41}+\dfrac{9}{10\cdot41}+\dfrac{7}{10\cdot57}\)
\(=\dfrac{20}{31\cdot35}+\dfrac{30}{35\cdot41}+\dfrac{45}{41\cdot50}+\dfrac{35}{50\cdot57}\)
\(=5\left(\dfrac{4}{31\cdot35}+\dfrac{6}{35\cdot41}+\dfrac{9}{41\cdot50}+\dfrac{7}{50\cdot57}\right)\)
\(=5\left(\dfrac{1}{31}-\dfrac{1}{35}+\dfrac{1}{35}-\dfrac{1}{41}+\dfrac{1}{41}-\dfrac{1}{50}+\dfrac{1}{50}-\dfrac{1}{57}\right)\)
\(=5\left(\dfrac{1}{31}-\dfrac{1}{57}\right)\)
Ta có: \(B=\dfrac{7}{19\cdot31}+\dfrac{5}{19\cdot43}+\dfrac{3}{23\cdot43}+\dfrac{11}{23\cdot57}\)
\(=\dfrac{14}{31\cdot38}+\dfrac{10}{38\cdot43}+\dfrac{6}{43\cdot46}+\dfrac{22}{46\cdot57}\)
\(=2\left(\dfrac{7}{31\cdot38}+\dfrac{5}{38\cdot43}+\dfrac{3}{43\cdot46}+\dfrac{11}{46\cdot57}\right)\)
\(=2\left(\dfrac{1}{31}-\dfrac{1}{38}+\dfrac{1}{38}-\dfrac{1}{43}+\dfrac{1}{43}-\dfrac{1}{46}+\dfrac{1}{46}-\dfrac{1}{57}\right)\)
\(=2\left(\dfrac{1}{31}-\dfrac{1}{57}\right)\)
Suy ra: \(\dfrac{A}{B}=\dfrac{5\left(\dfrac{1}{31}-\dfrac{1}{57}\right)}{2\left(\dfrac{1}{31}-\dfrac{1}{57}\right)}=\dfrac{5}{2}\)
29 tháng 4 2017
Giải
Ta có : \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{20^2}< \dfrac{1}{19.20}\)
\(\Rightarrow\)D < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{19.20}\)
Nhận xét: \(\dfrac{1}{1.2}=1-\dfrac{1}{2};\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4};...;\dfrac{1}{19.20}=\dfrac{1}{19}-\dfrac{1}{20}\)
\(\Rightarrow\) D< 1- \(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
D< 1 - \(\dfrac{1}{20}\)
D< \(\dfrac{19}{20}\)<1
\(\Rightarrow\)D< 1
Vậy D=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{5^2}\)<1
30 tháng 4 2017
A=\(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
A=\(\dfrac{1}{2^2.1}+\dfrac{1}{2^2.2^2}+\dfrac{1}{3^2.2^2}+...+\dfrac{1}{50^2.2^2}\)
A=\(\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}\right)\)
\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2.2}+\dfrac{1}{3.3}+...+\dfrac{1}{50.50}\right)\)
Ta có :
\(\dfrac{1}{2.2}< \dfrac{1}{1.2};\dfrac{1}{3.3}< \dfrac{1}{2.3};\dfrac{1}{4.4}< \dfrac{1}{3.4};...;\dfrac{1}{50.50}< \dfrac{1}{49.50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\right)\)Nhận xét :
\(\dfrac{1}{1.2}< 1-\dfrac{1}{2};\dfrac{1}{2.3}< \dfrac{1}{2}-\dfrac{1}{3};...;\dfrac{1}{49.50}< \dfrac{1}{49}-\dfrac{1}{50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{2^2}\left(1-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{4}.\dfrac{49}{50}\)<1
A<\(\dfrac{49}{200}< \dfrac{1}{2}\)
\(\Rightarrow A< \dfrac{1}{2}\)
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: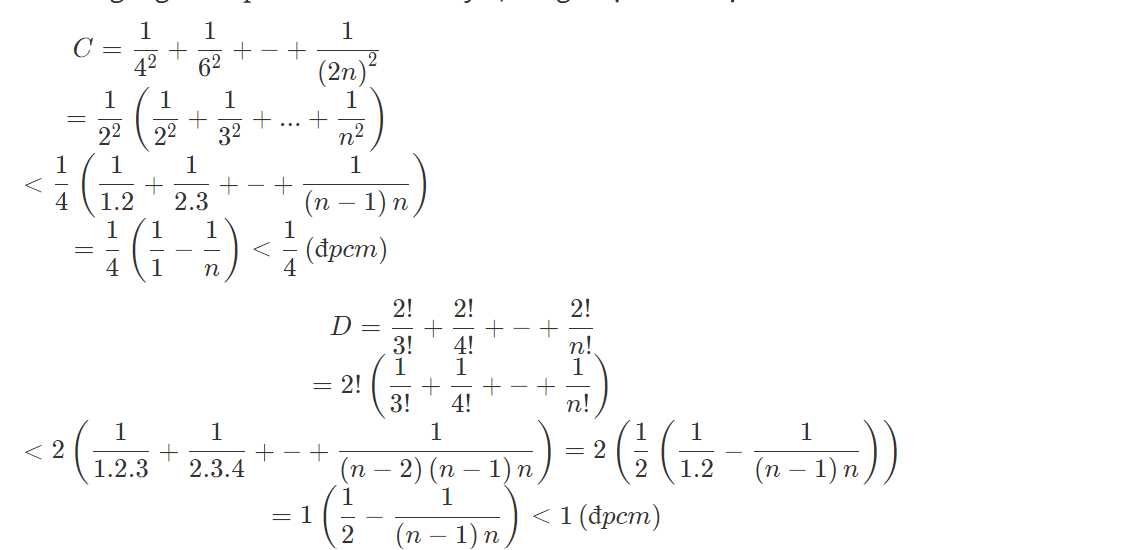 
29 tháng 7 2021
a) Ta có: \(A=\dfrac{4}{1\cdot4}+\dfrac{4}{4\cdot7}+\dfrac{4}{7\cdot10}+...+\dfrac{4}{31\cdot34}\)
\(=\dfrac{4}{3}\left(\dfrac{3}{1\cdot4}+\dfrac{3}{4\cdot7}+\dfrac{3}{7\cdot10}+...+\dfrac{3}{31\cdot34}\right)\)
\(=\dfrac{4}{3}\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{31}-\dfrac{1}{34}\right)\)
\(=\dfrac{4}{3}\left(1-\dfrac{1}{34}\right)\)
\(=\dfrac{4}{3}\cdot\dfrac{33}{34}=\dfrac{22}{17}\)
A.2=4/1.5+6/5.11+...+12/29.41
A.2=1-1/5+1/5-1/11+...+1/29-1/41
A.2=1-1/41
A.2=40/41
A=20/41
B.3=3/1.4+6/4.10+...+12/29.31
B.3=1-1/4+1/4-1/10+...+1/29-1/31
B.3=1-1/31
B.3=30/31
B=10/31
Vì 20/41.10/31 nên A>B
\(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(\Rightarrow2A=\dfrac{4}{1.5}+\dfrac{6}{5.11}+\dfrac{8}{11.19}+\dfrac{10}{19.29}+\dfrac{12}{29.41}\)
\(\Rightarrow2A=1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{41}\)
\(\Rightarrow2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(\Rightarrow A=\dfrac{40}{41}:2=\dfrac{20}{41}\)(1)
\(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(\Rightarrow3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(\Rightarrow3B=\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{31}\)
\(\Rightarrow3B=\dfrac{1}{1}-\dfrac{1}{31}=\dfrac{30}{31}\)
\(\Rightarrow B=\dfrac{30}{31}:3=\dfrac{10}{31}\)
\(\Rightarrow B=\dfrac{2}{2}.\dfrac{10}{31}=\dfrac{20}{62}\)
+)Ta có:\(\dfrac{20}{62}< \dfrac{20}{41}\Rightarrow B< A\)
Hay A>B(ĐPCM)
Chúc bn học tốt